Спектральное представление стационарных случайных процессов. Теорема Винера-Хинчина
Рассмотрим стационарный случайный процесс Х(t) c нулевым математическим ожиданием:
с некоторой детерминированной спектральной плотностью Важным вопросом является следующий: какими свойствами должны обладать случайные функции Свойства случайной спектральной плотности: 1) Прежде всего усредним мгновенные значения сигналов x(t) по ансамблю реализаций и приравняем его к нулю.
Это равенство будет выполняться тождественно при любом значении t, если потребовать выполнения условия 2) Возьмём комплексно сопряжённый сигнал, так что наряду с (6.19) справедливо равенство:
Запишем выражение функции корреляции процесса X(t), используя спектральные разложения случайных реализаций:
(6.21) Здесь во внутреннем подынтегральном выражении содержится множитель
Случайная спектральная плотность Введём в формулу (6.22) множитель пропорциональности, зависящий от частоты, и запишем это равенство таким образом:
Функция Подставив (6.23) в (6.21) приходим к важному результату:
Итак функция корреляции и спектр мощности стационарного случайного процесса связаны между собой преобразованиями Фурье. Формулы (6.24) и (6.25) составляют содержание теоремы Винера-Хинчина (1934 г. Хинчин А.Я. и Н. Винер). Для того чтобы выяснить физический смысл дисперсии, положим в (6.24)
Следует подчеркнуть различие между энергетическим спектром Свойства спектральной плотности мощности 1) По своему физическому смыслу спектр мощности вещественен и неотрицателен: Необходимо указать, что спектральная плотность мощности стационарного случайного процесса, будучи всегда вещественной, не содержит никакой информации о фазовых соотношениях между отдельными спектральными составляющими. Поэтому по спектру мощности принципиально невозможно восстановить какую либо отдельно взятую реализацию случайного процесса. 2) Поскольку
3. Целесообразно ввести так называемый односторонний спектр мощности
Функция
4. В технических расчётах часто вводят односторонний спектр мощности N(f), представляющий собой среднюю мощность случайного процесса, приходящуюся на интервал частот шириной в 1 Гц:
При этом, как легко видеть
Весьма важным параметром случайных процессов является интервал корреляции. Случайные процессы, как правило, обладают следующими свойствами: их функция корреляции стремится к нулю с увеличением временного сдвига Числовой характеристикой, служащей для оценки «скорости изменения» реализации случайного процесса, является интервал корреляции
Если известна информация о поведении какой-либо реализации «в прошлом», то возможен вероятностный прогноз случайного процесса на время порядка Ещё одним существенным параметром для случайного процесса является эффективная ширина спектра. Пусть исследуемый случайный процесс характеризуется функцией
Отсюда получается формула для эффективной ширины спектра:
Вне пределов указанной полосы спектральная плотность случайного процесса считается равной 0. Этой числовой характеристикой часто пользуются для инженерного расчёта дисперсии шумового сигнала: Если реализации случайного процесса имеют размерность напряжения (В), то относительный спектр мощности N имеет размерность
|

 . Отдельно взятая реализация этого процесса есть детерминированная функция, которую можно представить в виде обратного преобразования Фурье:
. Отдельно взятая реализация этого процесса есть детерминированная функция, которую можно представить в виде обратного преобразования Фурье: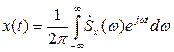 (6.19)
(6.19) . Для того, чтобы описать весь ансамбль реализаций, образующий процесс Х(t), нужно допустить, что спектральные плотности
. Для того, чтобы описать весь ансамбль реализаций, образующий процесс Х(t), нужно допустить, что спектральные плотности 
 . Итак, случайная спектральная плотность отдельных реализаций стационарного случайного процесса должна иметь нулевое математическое ожидание на всех частотах.
. Итак, случайная спектральная плотность отдельных реализаций стационарного случайного процесса должна иметь нулевое математическое ожидание на всех частотах. (6.20)
(6.20)
 , имеющий смысл функции корреляции случайной спектральной плотности. Для того чтобы функция
, имеющий смысл функции корреляции случайной спектральной плотности. Для того чтобы функция  не зависела от времени t, необходимо, как это видно из выражения (6.21) выполнение следующей пропорциональности:
не зависела от времени t, необходимо, как это видно из выражения (6.21) выполнение следующей пропорциональности: (6.22)
(6.22) стационарного процесса имеет специфическую структуру; ее значения отвечающие любым двум несовпадающим частотам, некоррелированы между собой. В то же время средний квадрат (дисперсия) случайной спектральной плотности неограниченно велик при любых частотах. Такой вид корреляционной связи называют дельта-коррелированностью.
стационарного процесса имеет специфическую структуру; ее значения отвечающие любым двум несовпадающим частотам, некоррелированы между собой. В то же время средний квадрат (дисперсия) случайной спектральной плотности неограниченно велик при любых частотах. Такой вид корреляционной связи называют дельта-коррелированностью. (6.23)
(6.23) называется спектральной плотностью мощности процесса Х(t) (спектром мощности). Если случайный сигнал является напряжением, то его спектр мощности имеет размерность
называется спектральной плотностью мощности процесса Х(t) (спектром мощности). Если случайный сигнал является напряжением, то его спектр мощности имеет размерность  , то есть размерность удельной мощности, выделяемой на единичном резисторе.
, то есть размерность удельной мощности, выделяемой на единичном резисторе. (6.24)
(6.24) (6.25)
(6.25) Тогда поскольку
Тогда поскольку  , получаем
, получаем (6.26)
(6.26) детерминированного импульсного сигнала u(t) и спектральной плотностью мощности
детерминированного импульсного сигнала u(t) и спектральной плотностью мощности  стационарного случайного процесса X(t). Функция
стационарного случайного процесса X(t). Функция  характеризует удельную меру мощности. Этот факт находит отражение и в разных физических размерностях данных функций.
характеризует удельную меру мощности. Этот факт находит отражение и в разных физических размерностях данных функций.
 чётная функция аргумента
чётная функция аргумента  , то соответствующий спектр мощности
, то соответствующий спектр мощности  представляет собой чётную функцию частоты
представляет собой чётную функцию частоты  . Отсюда следует, что пару преобразований Фурье (6.25), (6.26) можно записать, используя лишь интегралы в полубесконечных пределах:
. Отсюда следует, что пару преобразований Фурье (6.25), (6.26) можно записать, используя лишь интегралы в полубесконечных пределах: (6.27)
(6.27) (6.28)
(6.28) случайного процесса, определив его следующим образом:
случайного процесса, определив его следующим образом: (6.29)
(6.29) (6.30)
(6.30) (6.31)
(6.31)
 , тем меньше оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.
, тем меньше оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени. определяемый выражением:
определяемый выражением: (6.32)
(6.32) - экстремальное значение этой функции. Заменим мысленно данный случайный процесс другим процессом, у которого спектральная плотность мощности постоянна и равна
- экстремальное значение этой функции. Заменим мысленно данный случайный процесс другим процессом, у которого спектральная плотность мощности постоянна и равна  , выбираемой из условия равенства средних мощностей обоих процессов:
, выбираемой из условия равенства средних мощностей обоих процессов:
 (6.33)
(6.33)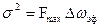 .
. .
.


