Быстрое преобразование Фурье
Как видно, из формул (7.4) и (7.5), чтобы вычислить ДПФ или ОДПФ последовательности из N элементов, требуется выполнить Выходом из положения является алгоритм быстрого преобразования Фурье (БПФ), предложенный в 60-х годах. Существенно сократить число операций удаётся за счёт того, что обработка входного массива сводится к нахождению ДПФ (или ОДПФ) массивов с меньшим числом членов. Предположим, что число отсчётов
И представим n-й коэффициент ДПФ в виде:
Из формулы видно, что первая половина коэффициентов ДПФ исходного сигнала с номерами от 0 до (N/2)-1 выражается через коэффициенты ДПФ двух частных последовательностей:
Учтём, что последовательности коэффициентов, относящихся к чётной и нечётной частям входного массива, являются периодическими с периодом N/2:
Кроме того, входящий в формулу (7.7) множитель при
Отсюда находим выражение для второй половины множества коэффициентов ДПФ
Формулы (7.7) и (7.8) лежат в основе алгоритма БПФ. Далее вычисления строят по итерационному принципу: последовательности отсчётов с чётными и нечётными номерами вновь разбивают на две части. Процесс продолжают до тех пор, пока не получается последовательность, состоящая из единственного элемента. ДПФ этого элемента совпадает с ним самим. Число операций, необходимых для вычисления БПФ оценивается как Выигрыш в скорости вычислений по сравнению с традиционным ДПФ достигает сотен и даже тысяч при достаточных длинах входных массивов.
|

 операций с комплексными числами. Если длины обрабатываемых массивов имеют порядок тысячи или более, то использовать эти алгоритмы дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств.
операций с комплексными числами. Если длины обрабатываемых массивов имеют порядок тысячи или более, то использовать эти алгоритмы дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств. , где Р - целое число. Разобьём входную последовательность
, где Р - целое число. Разобьём входную последовательность  на две части с чётными и нечётными номерами.
на две части с чётными и нечётными номерами.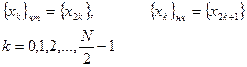 (7.6)
(7.6)
 n=0, 1, 2, …, (N/2)-1 (7.7)
n=0, 1, 2, …, (N/2)-1 (7.7)
 можно преобразовать так:
можно преобразовать так:
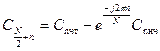
 (7.8)
(7.8)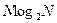 .
.


