Z-преобразование
При анализе и синтезе дискретных и цифровых устройств Z-преобразование играет такую же роль, как интегральные преобразования Фурье по отношению к непрерывным сигналам. Пусть
Эта сумма называется Z-преобразованием последовательности На основании формулы (7.9) можно непосредственно найти Z-преобразования сигналов с конечным числом отсчётов. Так простейшему дискретному сигналу с единственным отсчётом
Рассмотрим случай, когда в ряде (7.9) число слагаемых бесконечно велико. Возьмём дискретный сигнал
Аналогично получается Z-преобразование бесконечного дискретного сигнала
Данное выражение имеет смысл при |Z|> a Пусть x(z) – функция комплексной переменной Z. Замечательное свойство Z-преобразование состоит в том, что функция x(z) определяет всю бесконечную совокупность отсчётов ( Действительно, умножим обе части ряда (7.9) на множитель
а затем вычислим интегралы от обеих частей полученного равенства, взяв в качестве контура интегрирования произвольную замкнутую кривую, При этом воспользуемся фундаментальным положением из теоремы Коши:
Интегралы от всех слагаемых правой части обратятся в нуль, за исключением слагаемого с номером m, поэтому:
Данное выражение носит название обратное Z-преобразование. Важнейшие свойства Z-преобразования: 1. Линейность. Если 2. Z-преобразование смещённого сигнала. Рассмотрим дискретный сигнал
Таким образом, символ 3. Z-преобразование свёртки. Пусть x(z) и y(z) – непрерывные сигналы, для которых определена свёртка:
Применительно к дискретным сигналам по аналогии с (7.13) принято вводить дискретную свёртку
Подобную дискретную свёртку называют линейной Вычислим Z-преобразование дискретной свёртки:
Итак свёртке двух дискретных сигналов отвечает произведение Z-преобразований. Часть Раздел 1.Каналы электросвязи Тема1.1 Общие сведения о каналах электросвязи и их классификация
Каналом связи – называется совокупность средств, предназначенных для передачи сообщений (под “средством” понимают и технические устройства, и линию связи – физическую среду, в которой распространяется сигнал между пунктами связи). Классификация каналов связи возможна с использованием различных признаков. 1) В зависимости от назначения систем каналы связи делят на: телефонные, телевизионные, телеграфные, фототелеграфные, звукового вещания, телеметрические, смешанные и т.п. 2) В зависимости от того, распространяется ли сигнал между пунктами связи в свободном пространстве или по направляющим линиям, выделяют каналы радио и проводной связи (воздушные, кабельные, волоконно-оптические линии связи, волноводные СВЧ тракты и т. п.). 3) Более существенна классификация каналов электрической связи по диапазону используемых частот. Так на современных симметричных кабельных линиях связи применяют сигналы, занимающие полосы частот в диапазоне, ограниченном сверху частотой в несколько сотен килогерц. Дополнительные мероприятия по увеличению симметрии кабельных пар позволяют увеличить верхний предел используемого диапазона частот до тысячи килогерц. Коаксиальные кабели, являющиеся основой сетей магистральной дальней связи, пропускают в настоящее время диапазон частот до сотен мегагерц. На воздушных проводных линиях используют частоты не выше 150 кГц, ибо на более высоких частотах в этих линиях сильно сказывается мешающее действие аддитивных помех и резко возрастает затухание в линии. Радиосвязь осуществляется с помощью электромагнитных волн, распространяющихся в частично ограниченном (например, землёй и ионосферой) пространстве. В настоящее время в радиосвязи применяют частоты примерно от
Диапазон миллиметровых волн уже вплотную подходит к диапазону инфракрасных волн. В настоящее время благодаря созданию и внедрению в практику квантовых генераторов (лазеров и мазеров) освоен и диапазон световых волн(оптический диапазон). Для современного этапа развития техники связи характерна тенденция к переходу на все более высокие частоты. Это вызвано рядом причин, в частности, необходимостью повышать скорость передачи информации, возможностью получить остронаправленное излучение при необходимых размерах излучателей, меньшей интенсивностью атмосферных и многих видов промышленных помех в более высокочастотных диапазонах, возможностью применения помехоустойчивых систем модуляции и т.д. 4) Наибольший интерес для теории передачи сигналов представляет классификация каналов связи по характеру сигналов на входе и выходе канала. Различают каналы: а) дискретные, на входе и выходе которых сигналы дискретные. Таковы каналы, заданные между точками
б) непрерывные, на входе и выходе которых сигналы непрерывны. Примером может служить канал, заданный между выходом модулятора и входом демодулятора в любой системе связи; в) дискретные со стороны входа и непрерывные со стороны выхода, или наоборот. Такие каналы называются дискретно-непрерывными и непрерывно-дискретными (или полунепрерывными) (например, дискретно-непрерывные – это каналы, заданные между точками Всякий дискретный, или полунепрерывный канал содержит внутри себя непрерывный канал. Прохождение сигналов через каналы связи сопровождается изменениями (преобразованиями) этих сигналов. 5) С точки зрения передачи по каналу, важно подразделение преобразований сигнала на обратимые и необратимые. Обратимые преобразования не влекут за собой потери информации. При необратимых преобразованиях потери информации неизбежны. Для обратимых преобразований сигнала часто используют термин «искажение», а необратимые преобразования вызваны помехами (аддитивными и неаддитивными).
|

 – числовая последовательность, конечная или бесконечная, содержащая отсчётные значения некоторого сигнала. Поставим ей в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной Z:
– числовая последовательность, конечная или бесконечная, содержащая отсчётные значения некоторого сигнала. Поставим ей в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной Z: (7.9)
(7.9) . Свойства дискретных последовательностей чисел можно изучать, исследуя их Z-преобразования обычными методами математического анализа.
. Свойства дискретных последовательностей чисел можно изучать, исследуя их Z-преобразования обычными методами математического анализа. соответствует
соответствует  Если же, например,
Если же, например,  , то
, то
 образованный одинаковыми единичными отсчётами и служащий моделью обычной функции включения. Бесконечный ряд
образованный одинаковыми единичными отсчётами и служащий моделью обычной функции включения. Бесконечный ряд  является суммой геометрической прогрессии и сходится при любых Z, |Z|> 1. Суммируя прогрессию, получаем
является суммой геометрической прогрессии и сходится при любых Z, |Z|> 1. Суммируя прогрессию, получаем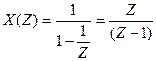
 , где а-некоторое вещественное число. Здесь
, где а-некоторое вещественное число. Здесь
 ).
). :
: (7.10)
(7.10)
 (7.11)
(7.11) - некоторые дискретные сигналы, причём известны соответствующие Z-преобразования x(z) и y(z), то сигналу
- некоторые дискретные сигналы, причём известны соответствующие Z-преобразования x(z) и y(z), то сигналу  будет отвечать преобразование
будет отвечать преобразование  при любых постоянных
при любых постоянных  и
и  . Доказательство проводится путём подстановки суммы в формулу (7.9).
. Доказательство проводится путём подстановки суммы в формулу (7.9). . Непосредственно вычисляя Z-преобразование, получаем следующий результат:
. Непосредственно вычисляя Z-преобразование, получаем следующий результат: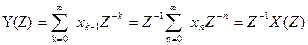 (7.12)
(7.12) служит оператором единичной задержки (на один интервал дискретизации) в Z-области.
служит оператором единичной задержки (на один интервал дискретизации) в Z-области. (7.13)
(7.13) – последовательность чисел общий член которой:
– последовательность чисел общий член которой: (7.14)
(7.14) (7.15)
(7.15) до
до  Гц. Этот диапазон принято в соответствии с десятичной классификацией подразделять следующим образом:
Гц. Этот диапазон принято в соответствии с десятичной классификацией подразделять следующим образом: Дециметровые (УКВ)
Сантиметровые
Дециметровые (УКВ)
Сантиметровые
 или
или  на схеме:
на схеме:
 ,
, 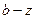 ; непрерывно-дискретные – это канал
; непрерывно-дискретные – это канал 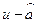 )
)


