Узкополосные случайные сигналы
Исследуем свойства узкополосных случайных сигналов, у которых спектральная плотность мощности имеет резко выраженный максимум вблизи некоторой частоты Рассмотрим стационарный случайный процесс x(t), односторонний спектр мощности которого
Мысленно сместим спектр процесса из окрестности частоты
В соответствии с исходным предположением об узкополосности процесса X(t) его спектр мощности
Особенно простой функция корреляции узкополосного процесса получается в случае, когда спектр мощности
Здесь коэффициент Тогда
Характерный вид функции корреляции (6.42) свидетельствует о том, что отдельные реализации узкополосного случайного процесса представляют собой квазигармонические колебания:
у которых как огибающая U(t), так и начальная фаза Представим реализацию (6.41) как сумму синфазной и квадратурной составляющих.
Предположение о медленности синфазной A(t) и квадратурной B(t) амплитуд позволяет весьма просто записать выражение для реализации сопряжённого процесса, вынеся медленные множители за знак преобразования Гильберта:
Отсюда получаем формулы для мгновенных значений реализации огибающей
и начальной фазы
Часто на практике ставится задача нахождения совместной плотности вероятности огибающей и начальной фазы узкополосного случайного процесса. При этом особенно удобно воспользоваться методом, основанном на переходе от узкополосного случайного процесса к его синфазной и квадратурной составляющим. Благодаря этому методу мы можем вычислить двумерную плотность вероятности
И плотность вероятности начальной фазы
Мгновенные значения амплитуды A(t) и B(t) образуют двумерный гауссов вектор, обе составляющие которого независимы и имеют одинаковые дисперсии
Теперь, чтобы получить искомую плотность вероятности
Якобиан такого преобразования
Поскольку в новых переменных
Теперь, используя формулы (6.49) и (6.53) можем найти плотность вероятности начальной фазы:
Введём замену переменной Тогда:
Таким образом, начальная фаза узкополосного случайного процесса распределена равномерно на отрезке На основании формул (6.48) и (6.53) определим одномерную плотность вероятности огибающей
Здесь так же целесообразно перейти к безразмерной переменной
Плотность вероятности мгновенных значений огибающей узкополосного случайного процесса, устанавливаемая выражением (6.55), (6.56) известна под названием закона Рэлея. Соответствующий график показывает, что наиболее вероятны некоторые средние (порядка
Проводя усреднение с помощью плотности вероятности (6.55) находим среднее значение огибающей и её дисперсию:
Располагая одномерной плотностью вероятности огибающей, можно решить ряд задач теории узкополосных случайных процессов, в частности, найти вероятность превышения огибающей некоторого заданного уровня. Случайные величины, распределенные по закону Рэлея, встречаются во многих задачах. Исследуем огибающую суммы гармонического сигнала и узкополосного нормального шума. Часто бывает необходимо определить статистические свойства сигнала, наблюдаемого на выходе некоторого частотно-избирательного устройства, например, резонансного усилителя. Будем считать, что помимо флуктуационного гауссова шума с центральной частотой Простейшей задачей является нахождение одномерной плотности вероятности огибающей суммарного колебания. Считая, что полезный сигнал
Легко проверить, что якобиан D этого преобразования равен U. Тогда, поскольку двумерная плотность вероятности:
В новых переменных имеем.
Теперь чтобы получить одномерную плотность вероятности огибающей, следует проинтегрировать правую часть формулы (6.60) по угловой координате в результате чего находим:
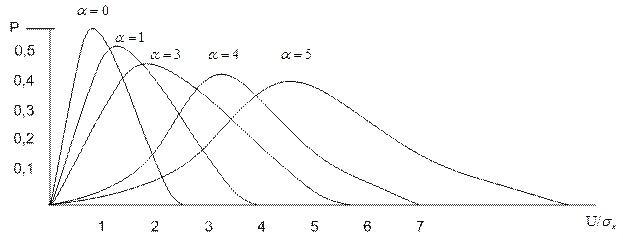
Данная формула выражает закон, получивший название закона Райса. Отметим, что при На рисунке представлены графики плотности вероятности случайной величины, распределённой по закону Райса при различных отношениях
Подставив это выражение в (6.61), имеем
Т.е. огибающая результирующего сигнала распределена в этом случае приближённо нормально с дисперсией
Раздел 7. Основные элементы цифровой обработки сигналов
|

 , отличной от нуля. Определим функцию корреляции узкополосного случайного процесса.
, отличной от нуля. Определим функцию корреляции узкополосного случайного процесса. концентрируется в окрестности некоторой частоты
концентрируется в окрестности некоторой частоты  (6.38)
(6.38) . Тогда формула (6.36) приобретает вид:
. Тогда формула (6.36) приобретает вид: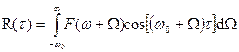 (6.39)
(6.39)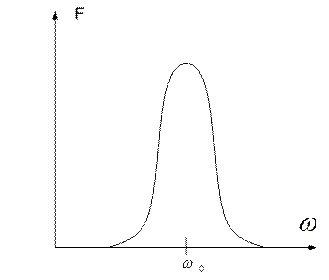
 , не внося ощутимой погрешности, и записать функцию корреляции в виде
, не внося ощутимой погрешности, и записать функцию корреляции в виде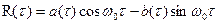 (6.40)
(6.40) , так что
, так что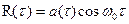 (6.41)
(6.41) играет роль огибающей, которая изменяется медленно по сравнению с множителем
играет роль огибающей, которая изменяется медленно по сравнению с множителем 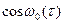 . Часто бывает удобным ввести нормированную огибающую
. Часто бывает удобным ввести нормированную огибающую 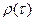 функции корреляции узкополосного случайного процесса, определив её с помощью равенства
функции корреляции узкополосного случайного процесса, определив её с помощью равенства  .
.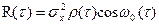 (6.42)
(6.42)
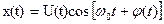 , (6.43)
, (6.43) являются случайными функциями, медленно (в масштабе
являются случайными функциями, медленно (в масштабе 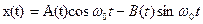 (6.44)
(6.44) (6.45)
(6.45)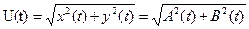 (6.46)
(6.46)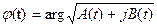 (6.45)
(6.45)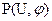 . Эта характеристика позволяет найти одномерную плотность вероятности огибающей:
. Эта характеристика позволяет найти одномерную плотность вероятности огибающей: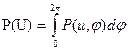 (6.48)
(6.48)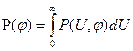 (6.49)
(6.49)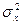 . Поэтому двумерная плотность вероятности.
. Поэтому двумерная плотность вероятности.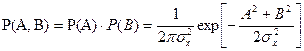 (6.50)
(6.50) следует выполнить функциональное преобразование, переводящее случайный вектор {A, B} в новую случайную совокупность
следует выполнить функциональное преобразование, переводящее случайный вектор {A, B} в новую случайную совокупность 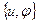 ,
, (6.51)
(6.51)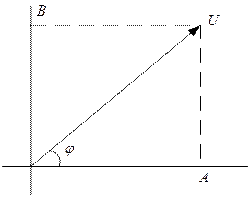
 (6.52)
(6.52)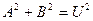 , искомая двумерная плотность вероятности:
, искомая двумерная плотность вероятности: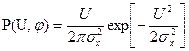 (6.53)
(6.53)
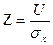
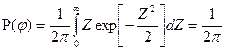 (6.54)
(6.54)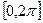
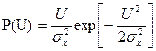 (6.55)
(6.55) (6.56)
(6.56)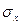 ) значения огибающей. В то же время маловероятно, чтобы огибающая принимала значения как близкие к нулю, так и значительно превосходящие среднеквадратичный уровень
) значения огибающей. В то же время маловероятно, чтобы огибающая принимала значения как близкие к нулю, так и значительно превосходящие среднеквадратичный уровень 
 (6.57)
(6.57)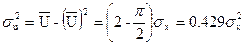 (6.58)
(6.58)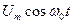 с известной амплитудой
с известной амплитудой  .
. , в то время как шум
, в то время как шум 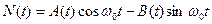 , запишем выражение реализации суммарного процесса X(t)
, запишем выражение реализации суммарного процесса X(t) 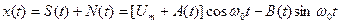 . Данный случайный процесс узкополосен, поэтому его реализация может быть выражена посредством медленно меняющихся огибающей U(t) и начальной фазы
. Данный случайный процесс узкополосен, поэтому его реализация может быть выражена посредством медленно меняющихся огибающей U(t) и начальной фазы 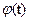 :
: . Очевидно между парами
. Очевидно между парами  имеется связь:
имеется связь: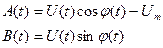 (6.59)
(6.59)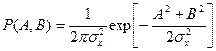
 (6.60)
(6.60)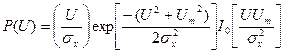 (6.61)
(6.61)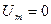 , т.е. в отсутствие детерминированного сигнала, закон Райса переходит в закон Рэлея.
, т.е. в отсутствие детерминированного сигнала, закон Райса переходит в закон Рэлея.
 Отметим, что если амплитуда детерминированного сигнала значительно превышает среднеквадратический уровень шума, т.е.
Отметим, что если амплитуда детерминированного сигнала значительно превышает среднеквадратический уровень шума, т.е.  > > 1 то при
> > 1 то при 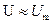 можно воспользоваться асимптотическим представлением модифицированных функций Бесселя с большим аргументом:
можно воспользоваться асимптотическим представлением модифицированных функций Бесселя с большим аргументом:
 (6.62)
(6.62)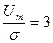 огибающая результирующего сигнала нормализуется.
огибающая результирующего сигнала нормализуется.


