Взаимная информация
Определим теперь информацию, содержащуюся в одном ансамбле относительно другого, например, в принятом сигнале относительно переданного сообщения. Для этого рассмотрим сообщение двух дискретных ансамблей A и B, вообще говоря, зависимых. Его можно интерпретировать как пару ансамблей сообщений, либо как ансамбли сообщения и сигнала, с помощью которого сообщение передаётся, либо как ансамбли сигналов на входе и выходе канала связи и т. д. Пусть P(ak, bl)совместная вероятность реализаций ak и bl. Cовместной энтропией ансамблей A и B будем называть:
Введём также понятие условной энтропии:
где P(ak / bl)- условная вероятность ak, если имеет место bl, здесь математические.. Из теоремы умножения вероятностей (2.8) Для условной энтропии справедливо двойное неравенство:
Рассмотрим два крайних случая: 1. Равенство 2. Другой крайний случай, когда В общем случае, что имеет место на практике, условная энтропия
Подставляя в эту формулу значения H(A) и H(A/B) выразим взаимную информацию через распределение вероятностей:
Если воспользоваться теоремой умножения
Взаимная информация измеряется в тех же единицах, что и энтропия. Величина Сформулируем основные свойства взаимной информации: 1. 2.
3. 4. 5. Полагая
Это позволяет интерпретировать энтропию источника как его собственную информацию, то есть информацию, содержащуюся в ансамбле Пусть Если
получим соответствующие равенства для энтропии и количества информации, рассчитанных не на одно сообщение, а на единицу времени. Величина Рассмотрим пример: если
Величина
Эффективное кодирование дискретных сообщений Применим полученные результаты к проблеме кодирования дискретных сообщений. Пусть
где Будем рассматривать для простоты только двоичный код, при котором алфавит
Но это отношение представляет среднее число кодовых символов, приходящихся на одно элементарное сообщение. Таким образом, для возможности кодирования и однозначного декодирования сообщения необходимо, чтобы среднее число двоичных символов на сообщение было не меньше энтропии Одна из основных теорем теории информации утверждает, что оно “почти достаточно”. Точнее, содержание теоремы кодирования для источника заключается в том, что передавая двоичные символы со скоростью
где Эта теорема почти тривиальна, если источник передаёт сообщения независимо и равновероятно. В этом случае Таким образом можно закодировать сообщения любого источника с объёмом алфавита Рассмотрим несколько примеров. Так, если элементарными сообщениями являются русские буквы Разумеется, таким же равномерным кодом можно закодировать и буквы в связном русском тексте, и именно так часто поступают на практике. Но можно обойтись значительно меньшим числом символов на букву. Для русского литературного текста Существует довольно много способов сжатия сообщений или сокращения избыточности текста. Так, например: ”Эта фр. напис. сокращ. и тем не м. мож. надеят., что Вы пойм. её прав.” В предыдущей фразе удалось уменьшить число букв, а следовательно и символов, если её кодировать равномерным кодом почти на 40%. Другая возможность заключается в том, чтобы кодировать не отдельные буквы, а целые слова. Дальнейшее сжатие сообщений возможно путём применения неравномерного кода, если более короткие последовательности используются для более частых букв (слов) и более длинные – для более редких. Заметим, что эта идея неравномерного кодирования впервые нашла применение в телеграфном коде Морзе, в котором наиболее короткие комбинации использованы для часто встречающихся букв (е, и, т, с, а). Применение неравномерного кода позволяет снизить избыточность, вызванную неравной вероятностью между сообщениями. Разработано много методов эффективного кодирования для различных источников. Задача эффективного кодирования наиболее актуальна не для передачи текста, а для других источников со значительно большей избыточностью. К ним относятся, например, телевизионные передачи (промышленное телевидение), некоторые телеметрические системы, в которых возможно сжатие в десятки раз, фототелеграфия. Тема 2.4. Информация в непрерывных сигналах Обобщим теперь понятия энтропии и взаимной информации на ансамбли непрерывных сигналов. Пусть Разобьём область значений
Будем теперь увеличивать точность определения значения
(2.19) Второй член в полученном выражении стремится к Обратим внимание на первый член в данной формуле. Он является конечным и определяется плотностью распределения вероятности
Попытаемся теперь определить взаимную информацию между двумя непрерывными случайными величинами
При этом никаких явных бесконечностей не появилось, и действительно, в обычных случаях взаимная информация оказывается конечной. С помощью простых преобразований её можно представить и в таком виде: (2.22) Здесь В качестве примера найдём дифференциальную энтропию случайной величины
где Подставив (2.23) в (2.20), найдём:
Первый интеграл по общему свойству плотности вероятности равен 1, а второй – по определению дисперсии равен
Таким образом, диффиринциал энтропия гауссовский случайной величины не зависит от её математического ожидания и монотонно возрастает с увеличением дисперсии. В заключение укажем одно важное свойство нормального распределения: из всех непрерывных случайных величин
Тема 2.5. Пропускная способность канала связи В любой системе связи через канал передаётся информация. Её скорость передачи зависит не только от самого канала, но и от свойств подаваемого на его вход сигнала и поэтому не может характеризовать канал как средство передачи информации. Найдём способ оценки способности канала передавать информацию. Для каждого источника количество информации, переданной по каналу принимает своё значение. Максимальное количество переданной информации, взятое по всевозможным источникам входного сигнала, характеризует сам канал и называется пропускной способностью канала в расчёте на один символ:
(где максимизация производится по всем многомерным распределениям вероятностей Р(А)) Можно также определить пропускную способность С канала в расчёте на единицу времени.
Вычислим пропускную способность симметричного канала без памяти
Величина Первое из этих значений возникает с вероятностью Р, а второе – с вероятностью (1-Р). К тому же, поскольку рассматривается канал без памяти, результаты приёма отдельных символов независимы друг от друга. Поэтому
Следовательно Н(В/А) не зависит от распределения вероятности в ансамбле А, а определяется только переходными вероятностями канала. Это свойство сохраняется для всех моделей с аддитивным шумом. Подставив (2.27) в (2.26) получим:
Поскольку в правой части только член Н(В) зависит от распределения вероятности Р(А), то максимизировать необходимо именно его. Максимальное значение Н(В) равно log m и реализуется оно тогда, когда все принятые символы
При этом
Отсюда пропускная способность в расчёте на единицу времени
Для двоичного симметричного канала (m=2) пропускная способность в двоичных единицах в единицу времени
Зависимость При Р=1/2 пропускная способность двоичного канала С=0, поскольку при такой вероятности ошибки последовательность выходных двоичных символов можно получить совсем не передавая сигналы по каналу, а выбирая их наугад (например, по результатам бросания монеты), то есть при Р=1/2 последовательности на выходе и входе канала независимы. Случай С=0 называется обрывом канала. То, что пропускная способность при P=1 в двоичном канале такая же, как при Р=0 (канал без шумов), объясняется тем, что при Р=1 достаточно все выходные символы инвертировать (то есть заменить 0 на 1 и 1 на 0), чтобы правильно восстановить входной сигнал. Пропускная способность непрерывного канала вычисляется аналогично. Пусть, например, канал имеет ограниченную полосу пропускания шириной F. Тогда сигналы U(t) и Z(t) соответственно на входе и выходе канала по теореме. Котельникова определяются своими отсчётами, взятыми через интервал 1/(2F), и поэтому информация, проходящая по каналу за некоторое время Т, равна, сумме количества информации, переданной за каждый такой отсчёт. Пропускная способность канала на один такой отсчёт:
Здесь U и Z – случайные величины – сечения процессов U(t) и Z(t) на входе и выходе канала соответственно и максимум берётся по всем допустимым входным сигналам, то есть по всем распределениям U. Пропускная способность С определяется как сумма значений Вычислим пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим полосу пропускания шириной F, если средняя мощность сигнала Z=U+N (2.33) Так как N имеет нормальное распределение с нулевым математическим ожиданием, то и условная плотность вероятности Пропускная способность на один отсчёт определятся по формуле (2.32):
Согласно (2.24) условная дифференциальная энтропия h(Z/U) нормального распределения
Таким образом, дисперсиия
Откуда
Переходя к пропускной способности С в расчёте на секунду, заметим, что информация, переданная за несколько отсчётов, максимальна в том случае, когда отсчёты сигналов независимы. Этого можно достичь, если сигнал U(t) выбрать так, чтобы его спектральная плотность была равномерной в полосе F. Отсчёты разделённые интервалами, кратными 1/(2F), взаимно некоррелированы, а для гауссовских величин некоррелированность означает независимость. Поэтому пропускную способность С (за секунду) можно найти, сложив пропускные способности (2.35) для 2F независимых отсчётов:
Она реализуется, если U(t) – гауссовский процесс с равномерной спектральной плотностью в полосе частот F (квазибелый шум). Из (2.36) видно, что если бы мощность сигнала Соотношение (2.36) называется формулой Шеннона. Эта формула имеет важное значение в теории информации, так как определяет зависимость пропускной способности рассматриваемого непрерывного канала от таких его технических характеристик, как ширина полосы пропускания и отношение сигнал шум. Формула Шеннона указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. Однако поскольку С зависит от F линейно, а от Максимальный объём информации, которую можно в среднем передать по непрерывному каналу за время Для гауссовского канала
Заметим, что при
Тема 2.6. Теорема К. Шеннона
Пропускная способность канала характеризует потенциальные возможности передачи информации. Они раскрываются в фундаментальной, теореме теории информации, известной как оснавная теорема кодирования К. Шеннона. Применительно к дискретному источнику она формулируется так: если производительность источника сообщений Н(А) меньше пропускной способности канала С:
то существует способ кодирования (преобразования сообщения в сигнал на входе) и декодирования (преобразования сигнала в сообщение на выходе канала), при при котором вероятность ошибочного декодирования и ненадёжность могут быть сколь угодно малы. Если же Рассмотрим содержание теоремы Шеннона. Как отмечалось, для восстановления по пришедшему сигналу переданного сообщения необходимо, чтобы сигнал содержал о нём информацию, равную энтропии сообщения. Следовательно, для правильной передачи сообщения необходимо, чтобы скорость передачи информации была не меньше производительности источника. Так как по определению скорость передачи информации не превышает пропускной способности, то неравенство Но является ли это условие достаточным? Конечно, при C> H’(A) можно передавать такие сигналы, что Положительный ответ на этот вопрос очевиден в тривиальном случае, когда в канале нет помех и сигнал В принимается безошибочно. При этом Теорема Шеннона даёт на этот вопрос почти положительный ответ, с той лишь поправкой, что скорость «утечки информации» (или ненадёжность) не равна в точности нулю, но может быть сделана сколь угодно малой. соответственно сколь угодно малой может быть сделана вероятность ошибочного декодирования. При этом, чем меньше допустимая вероятность ошибочного декодирования, тем сложнее должен быть код. Если бы двоичный канал был без помех и допускал передачу двоичных символов со скоростью
В этом случае данная теорема свелась бы к теореме о кодировании источника. Однако основной интерес представляет более общий случай двоичного канала с помехами. Его пропускная способность С меньше той скорости Теорема кодирования Шеннона справедлива для весьма широкого класса каналов. В частности, она верна и для передачи дискретных сообщений по непрерывному каналу. В этом случае под кодированием понимают отбор некоторого количества реализаций U(t) входного сигнала на интервале Т и сопоставление с каждой из них последовательности элементарных сообщений, выдаваемой источником за тот же интервал Т. Подчеркнём важный результат, следующий из теоремы: верность связи тем выше, чем длиннее кодируемый отрезок сообщения (а следовательно, и больше задержка при приёме информации), и чем менее эффективно используется пропускная способность канала (чем больше разность
Тема 2.7. Информация в непрерывных сообщениях. Эпсилон-энтропия
Для передачи непрерывного сообщения с абсолютной точностью нужно было бы передать бесконечно большое количество информации, что, разумеется, невозможно сделать за конечное время, пользуясь каналом с конечной пропускной способностью. Точно так же непрерывное
|

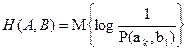 (2.6)
(2.6) (2.7)
(2.7) следует, что
следует, что  .
. (2.9)
(2.9) имеет место в том случае, когда, зная реализацию
имеет место в том случае, когда, зная реализацию  , можно точно установить реализацию
, можно точно установить реализацию  . Другими словами,
. Другими словами,  имеет место, если события
имеет место, если события  меньше безусловной
меньше безусловной  и знание реализации
и знание реализации  количеством информации, содержащейся в
количеством информации, содержащейся в  и
и  :
: (2.10)
(2.10) (2.11)
(2.11) , то можно записать
, то можно записать  :
: (2.12)
(2.12) , причём равенство имеет место тогда и только тогда, когда
, причём равенство имеет место тогда и только тогда, когда 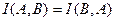 , то есть
, то есть  (2.13)
(2.13)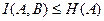 , причём равенство имеет место, когда по реализации
, причём равенство имеет место, когда по реализации  , причём равенство имеет место, когда по реализации
, причём равенство имеет место, когда по реализации  и учитывая, что
и учитывая, что  получим:
получим: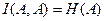 (2.14)
(2.14) в том и только в том случае, когда преобразование
в том и только в том случае, когда преобразование  обратимо. При необратимом преобразовании
обратимо. При необратимом преобразовании  и разность
и разность  можно назвать потерей информации при преобразовании
можно назвать потерей информации при преобразовании  - среднее время передачи одного сообщения, то разделив на
- среднее время передачи одного сообщения, то разделив на  ,
,  , (2.15)
, (2.15) называется скоростью передачи информации от
называется скоростью передачи информации от  - ансамбль сигналов на входе дискретного канала, а
- ансамбль сигналов на входе дискретного канала, а  - ансамбль сигналов на его выходе, то скорость передачи информации по каналу.
- ансамбль сигналов на его выходе, то скорость передачи информации по каналу. (2.16)
(2.16)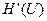 - производительность источника передаваемого сигнала
- производительность источника передаваемого сигнала  “производительность канала”, то есть полная собственная информация о принятом сигнале за единицу времени.
“производительность канала”, то есть полная собственная информация о принятом сигнале за единицу времени.
 представляет собой скорость “утечки” информации при прохождении через канал, а
представляет собой скорость “утечки” информации при прохождении через канал, а  - скорость передачи посторонней информации, не имеющий отношения к
- скорость передачи посторонней информации, не имеющий отношения к 

 и производительностью
и производительностью  . Для передачи по дискретному каналу нужно преобразовать сообщения в последовательность кодовых сигналов
. Для передачи по дискретному каналу нужно преобразовать сообщения в последовательность кодовых сигналов  . Следовательно, необходимым условием для кодирования является
. Следовательно, необходимым условием для кодирования является  или, обозначая через
или, обозначая через  длительность кодового символа, через
длительность кодового символа, через  длительность элементарного сообщения,
длительность элементарного сообщения,  , или
, или , (2.17)
, (2.17)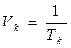 - число кодовых символов, a
- число кодовых символов, a  - число сообщений, передаваемых в секунду.
- число сообщений, передаваемых в секунду. бит. Поэтому, необходимое условие сводится к тому, что:
бит. Поэтому, необходимое условие сводится к тому, что: (2.18)
(2.18) симв/с можно закодировать сообщения так, чтобы передавать их со скоростью:
симв/с можно закодировать сообщения так, чтобы передавать их со скоростью: (сообщений в секунду),
(сообщений в секунду),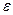 - сколь угодно малая величина.
- сколь угодно малая величина. и, если ещё к тому же
и, если ещё к тому же  -целая степень двух
-целая степень двух  , то
, то  .
. двоичных символов на элементарное сообщение. Если, однако, сообщения передаются не равновероятно, и (или) не независимо, то
двоичных символов на элементарное сообщение. Если, однако, сообщения передаются не равновероятно, и (или) не независимо, то  и возможно более экономное кодирование с затратой
и возможно более экономное кодирование с затратой  символов на сообщение. Относительная экономия символов при этом окажется равной
символов на сообщение. Относительная экономия символов при этом окажется равной  . Таким образом, избыточность определяет достижимую степень ”сжатия сообщения”.
. Таким образом, избыточность определяет достижимую степень ”сжатия сообщения”.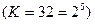 и они передаются равновероятно и независимо, то
и они передаются равновероятно и независимо, то  . Каждую букву можно закодировать последовательностью из пяти двоичных символов, поскольку существует 32 такие последовательности.
. Каждую букву можно закодировать последовательностью из пяти двоичных символов, поскольку существует 32 такие последовательности. и, следовательно, возможен способ эффективного кодирования (или кодирования со сжатием сообщения), при котором в среднем на букву русского текста будет затрачено немногим более 1, 5 двоичных символа, то есть на 70% меньше, чем при примитивном коде.
и, следовательно, возможен способ эффективного кодирования (или кодирования со сжатием сообщения), при котором в среднем на букву русского текста будет затрачено немногим более 1, 5 двоичных символа, то есть на 70% меньше, чем при примитивном коде. - случайная величина (сечение или отсчёт случайного сигнала), определённая в некоторой непрерывной области, и её распределение вероятностей характеризуется плотностью
- случайная величина (сечение или отсчёт случайного сигнала), определённая в некоторой непрерывной области, и её распределение вероятностей характеризуется плотностью  .
. . Вероятность того, что
. Вероятность того, что  ,
,  , приблизительно равна
, приблизительно равна  , причём приближение тем точнее, чем меньше интервал
, причём приближение тем точнее, чем меньше интервал  . Если значения
. Если значения 
 должна получиться энтропия непрерывной случайной величины:
должна получиться энтропия непрерывной случайной величины:
 и совершенно не зависит от распределения вероятностей
и совершенно не зависит от распределения вероятностей 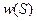 . Его называют дифференциальной энтропией и обозначают
. Его называют дифференциальной энтропией и обозначают  :
: (2.20)
(2.20) и
и  , заменим эти непрерывные величины дискретными так же, как это делалось при выводе формулы
, заменим эти непрерывные величины дискретными так же, как это делалось при выводе формулы 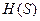 . Исходя из этого выражения можно определить взаимную информацию между непрерывными величинами
. Исходя из этого выражения можно определить взаимную информацию между непрерывными величинами  (2.21)
(2.21)
 - условная дифференциальная энтропия. Легко убедиться, что основные свойства взаимной информации остаются справедливыми и в данном случае.
- условная дифференциальная энтропия. Легко убедиться, что основные свойства взаимной информации остаются справедливыми и в данном случае. с нормальным распределением вероятности:
с нормальным распределением вероятности: , (2.23)
, (2.23) математическое ожидание, а
математическое ожидание, а  - дисперсия
- дисперсия 
 (2.24)
(2.24) бит/ симв.
бит/ симв. (2.25)
(2.25)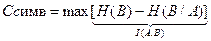 (2.26)
(2.26) в данном случае легко вычисляется, поскольку условная (переходная) вероятность
в данном случае легко вычисляется, поскольку условная (переходная) вероятность  принимает только два значения:
принимает только два значения:  , если
, если  и (1-Р), если
и (1-Р), если  .
. (2.27)
(2.27) (2.28)
(2.28) равновероятны и независимы друг от друга. Легко убедиться, что это условие удовлетворяется, если входные символы равновероятны и независимы, поскольку в этом случае
равновероятны и независимы друг от друга. Легко убедиться, что это условие удовлетворяется, если входные символы равновероятны и независимы, поскольку в этом случае
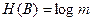 и
и (2.29)
(2.29) (2.30)
(2.30) (2.31)
(2.31)
 от Р согласно формуле (2.31)
от Р согласно формуле (2.31) (2.32)
(2.32) , взятая по всем отсчётам за секунду. При этом разумеется дифференциальные энтропии в (2.35) должны вычисляться с учётом вероятностных связей между отсчётами.
, взятая по всем отсчётам за секунду. При этом разумеется дифференциальные энтропии в (2.35) должны вычисляться с учётом вероятностных связей между отсчётами. . Мощность (дисперсию) шума в полосе F обозначим
. Мощность (дисперсию) шума в полосе F обозначим  . Отсчёты выходного и входного сигналов, а также шума N связаны равенством:
. Отсчёты выходного и входного сигналов, а также шума N связаны равенством: при фиксированном U будет так же нормальной – с математическим ожиданием U и дисперсией
при фиксированном U будет так же нормальной – с математическим ожиданием U и дисперсией 
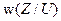 не зависит от математического ожидания и равна
не зависит от математического ожидания и равна 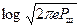 . Поэтому для нахождения
. Поэтому для нахождения  , при которой максимизируется h(Z). Из (2.33) учитывая, что U и N независимые случайные величины имеем для дисперсий
, при которой максимизируется h(Z). Из (2.33) учитывая, что U и N независимые случайные величины имеем для дисперсий
 фиксирована, так как
фиксирована, так как  (2.34)
(2.34) (2.35)
(2.35) (2.36)
(2.36) в канале равно нулю. С ростом этого отношения пропускная способность увеличивается неограниченно, однако медленно, вследствие логарифмической зависимости.
в канале равно нулю. С ростом этого отношения пропускная способность увеличивается неограниченно, однако медленно, вследствие логарифмической зависимости. – по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, не выгодно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания.
– по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, не выгодно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания. ,
, 
 (2.37)
(2.37) Выражение (2.37) совпадает с характеристикой названной ёмкостью (объёмом) канала.
Выражение (2.37) совпадает с характеристикой названной ёмкостью (объёмом) канала. (A)< C, (12.38)
(A)< C, (12.38) достигнет значения H’(A). Но
достигнет значения H’(A). Но  , и если между А и В установлено взаимно однозначное соответствие, то по принятому сигналу можно однозначно восстановить сообщение. В общем же случае в канале имеются помехи и сигнал В принимается с ошибками, так что
, и если между А и В установлено взаимно однозначное соответствие, то по принятому сигналу можно однозначно восстановить сообщение. В общем же случае в канале имеются помехи и сигнал В принимается с ошибками, так что  . Отсюда следует, что даже если
. Отсюда следует, что даже если 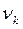 символ/с, то пропускная способность в расчёте на секунду была бы
символ/с, то пропускная способность в расчёте на секунду была бы (2.39)
(2.39) . Это, означает, что передаваемые символы не равновероятны и (или) не независимы, то есть код должен иметь избыточность в отличие от эффективного кода, пригодного для канала без помех. Это значит, что при кодировании сообщений последовательностью кодовых символов используют не все возможные кодовые последовательности.
. Это, означает, что передаваемые символы не равновероятны и (или) не независимы, то есть код должен иметь избыточность в отличие от эффективного кода, пригодного для канала без помех. Это значит, что при кодировании сообщений последовательностью кодовых символов используют не все возможные кодовые последовательности. , определяющая «запас пропускной способности» канала). Итак, существует возможность обмена между верностью, задержкой и эффективностью системы. С увеличением Т существенно возрастает сложность кодирования и декодирования (число операций, число элементов и стоимость аппаратуры). Поэтому практически чаще всего предпочитают иметь умеренное значение задержек Т, которые кстати, не во всех системах связи можно произвольно увеличивать, и добиваются повышения верности за счёт менее полного использования пропускной способности канала.
, определяющая «запас пропускной способности» канала). Итак, существует возможность обмена между верностью, задержкой и эффективностью системы. С увеличением Т существенно возрастает сложность кодирования и декодирования (число операций, число элементов и стоимость аппаратуры). Поэтому практически чаще всего предпочитают иметь умеренное значение задержек Т, которые кстати, не во всех системах связи можно произвольно увеличивать, и добиваются повышения верности за счёт менее полного использования пропускной способности канала.


