Потенциальная помехоустойчивость систем с различными видами манипуляции
Определим потенциальную помехоустойчивость для двоичной системы с аддитивным белым шумом, когда при приёме точно известны оба ожидаемых сигнала:
При выполнении неравенства (3.36) оптимальный приёмник регистрирует символ 1, соответствующий сигналу
которое приводится к следующему виду:
Аналогичное соотношение получится, если предположить, что передаётся символ 0. Следовательно, в обоих случаях вероятности ошибки равны: Введём обозначения:
Тогда: Если N(t) – нормальный стационарный белый шум с нулевым средним и односторонней спектральной плотностью мощности Учитывая выражение для функции корреляции белого шума и фильтрующее свойство
Тогда вероятность выполнения неравенства (13.40), то есть вероятность ошибки будет равна
где произведена замена переменной
Функция Ф
Таким образом, при заданной интенсивности помехи Помехоустойчивость выше, (вероятность ошибки меньше), у той системы, у которой больше эквивалентная энергия используемых сигналов. Эти важнейшие результаты получил академик В. А. Котельников. Сравним различные виды манипуляции для двоичной системы. 1) АМн – амплитудная манипуляция
где, 2) ЧМн – частотная манипуляция.
Максимально возможные значения 3) ФМн – фазовая манипуляция
Из сравнения различных видов манипуляции видно, что при переходе от системы АМн к системе с ЧМн (с ортогональными сигналами) можно обеспечить неизменное качество связи (вероятность ошибки) при понижении средней мощности передатчика в 2 раза, то есть получить энергетический выигрыш в 2 раза (или на 3 дБ). При переходе же к системе с ФМн (с противоположными сигналами) получается энергетический выигрыш ещё в 2 раза – по сравнению с ЧМн и в 4 раза – по сравнению с АМн. Если же сравнение вести не по пиковой, а по средней мощности, то переход от АМн к ЧМн не даёт энергетического выигрыша, поскольку при ЧМн средняя мощность равна максимальной, а при АМн – вдвое меньше максимальной (если Однако помехоустойчивость систем с ЧМн значительно выше по сравнению с АМн. Это объясняется не увеличением потенциальной помехоустойчивости, которая для обеих систем одинакова, а главным образом тем, что оптимальная решающая схема для ЧМн реализуется с довольно большой точностью, а при АМ этому препятствует невозможность обеспечить точное оптимальное значение ненулевого порогового уровня Система ФМн, как и другие системы с противоположенными сигналами, обеспечивает максимальную для двоичной системы потенциальную помехоустойчивость. Однако реализация демодулятора для когерентного приёма ФМн встречает определённые трудности. При построении демодулятора с активным фильтром возникает проблема поддержания равенства фаз опорного генератора приходящего сигнала. Если пытаться строить его на основе согласованного фильтра, то возникает ещё более трудная задача когерентного отсчёта. Задача выделения опорного сигнала особенно затрудняется при ФМн, так как, если элементы Главным же недостатком ФМн является возможность перескока фазы опорного сигнала, вследствие чего даже при отсутствии аддитивной помехи в канале символы инвертируются (нули в 1, а 1 Эффективный метод устранения этого явления был найден путём перехода к относительным методам модуляции предложенным Н.Т. Петровичем в 1957 году. Они сводятся к модуляции информационного параметра передаваемой посылки элемента сигнала относительно того же параметра предшествующей посылки. При относительной фазовой манипуляции (ОФМн) сообщение содержится не в абсолютном значении фазы элемента сигнала, а в разности фаз двух соседних элементов, при этом символ 1 передаётся повторением этой реализации сигнала, которая имела место в качестве предыдущего элемента, а символ 0 – передачей реализации с обратной фазой, либо наоборот. Сигналы ОФМн могут приниматься различными методами. Рассмотрим квазикогерентный приём сигналов ОФМн, называемый методом сравнения полярностей. Систему ОФМн можно рассматривать как обычную систему с ФМн, но со специальным перекодированием символов. Это означает, что оптимальный приём сигналов ОФМн, можно осуществить следующей схемой. Перекодирование выполняется сравнением полярностей напряжения на выходе интегратора для двух соседних элементов, для чего требуется задержка выходных символов в ячейке памяти (ЯП) на время Т.
Так как ОФМн – система с активной паузой, то пороговый уровень в демодуляторе – нулевой и решающее устройство превращается в дискриминатор полярности (ДП). Полярности соседних элементов сравниваются в схеме сравнения полярностей (ССП), которая представляет собой обычный перемножитель. Символ 1 регистрируется на выходе приёмника, например, при совпадении полярности двух соседних посылок; символ 0 – если эти полярности различны. При таком методе приёма перескок фазы опорного сигнала (при отсутствии помехи в канале) вызывает ошибку только в одном символе. Последующие же символы регистрируются правильно. Определим вероятность ошибки в системе ОФМн при учёте флуктуационной помехи в канале при когерентном приёме. Вероятность Рофмнн ошибочной регистрации символов в системе ОФМн не совпадает с вероятностью появления ошибок на выходе фазового детектора или, что то же самое, с вероятностью ошибок в системе «классической» фазовой манипуляции, определяемой (3.47). Очевидно, что ошибочная регистрация символа (при приёме методом сравнения полярностей) возможна в результате одного из двух несовместимых событий: а) знак данного элемента принят ошибочно, а предыдущего – верно; б) знак данного элемента принят верно, предыдущего – ошибочно. Каждое из этих событий имеет вероятность Рфмн (1 - Рфмн). Таким образом:
В нормальных условиях эксплуатации, когда требуется
Таким образом, «платой» за устранение обратной работы является удвоение вероятности ошибки, обусловленной шумом в канале. Для недвоичных систем (
где
3.9 Приём сигналов с неопределённой фазой (некогерентный приём)
В тех случаях, когда не удаётся точно оценить фазу или эта оценка требует применения сложных устройств, используют алгоритм, построенный в предположении, что начальная фаза приходящего сигнала неизвестна и может принимать любое значение на интервале
где Введём обозначения:
Тогда можно записать:
где (3.55) Вместо того, чтобы сравнить отношения правдоподобия
При выполнении этого неравенства регистрируется 1, в противном случае – 0. Величины
Здесь Величины
Алгоритм (3.56) и соответственно его реализация существенно упрощаются для систем с равными энергиями (
Для двоичной системы правило (3.58) упрощается и сводится к проверке одного неравенства
При его выполнении регистрируется символ 1, в противном случае – 0. При реализации алгоритма (3.59) не нужны блоки НУ и блоки вычитания. Схемы упрощаются. Исследования вероятности ошибок в канале с неопределённой фазой и аддитивным гауссовским шумом при поэлементном приёме показало, что минимальную вероятность ошибки обеспечивает система с равными энергиями, у которой сигналы удовлетворяют условиям ортогональности в усиленном смысле. Два сигнала x(t) и y(t) называются ортогональными в усиленном смысле, если соответствующие им аналитические сигналы
Если N(t) – нормальный стационарный белый шум с нулевым средним и односторонней спектральной плотностью мощности
Вероятность приёма символа 0 при передаче символа 1 определяется формулой:
Используя методы теории вероятностей данное выражение можно преобразовать. В итоге получаем:
Такова же будет вероятность приёма символа 1 при передаче 0. Для АМн: Для ОФМн (по методу сравнения фаз):
Рассмотрим теперь, как осуществляется оптимальный приём в канале, где флуктуирует не только начальная фаза, но и амплитуда сигнала. Задача синтеза оптимального демодулятора дискретных сигналов, с неопределённой фазой и амплитудой решается аналогично задаче синтеза сигналов с неопределённой фазой. Однако условия приёма несколько отличаются. Математическая модель такого сигнала называется гауссовским каналом с общими замираниями.
Сигнал на выходе канала флуктуирует как по начальной фазе, так и по амплитуде. Это приводит к некоторому изменению выражений для функции правдоподобия и для правила принятия решений. Однако структура оптимального приёмника совпадает со структурой оптимального приёмника дискретных сигналов с неопределённой начальной фазой. Изменяются только значения пороговых уровней на входах устройств сравнения. Помехоустойчивость приёма дискретных сообщений при замираниях сигнала получена для случая приёма двоичных ортогональных сигналов с равными энергиями. Замирания считаются медленными, когда на протяжении единичного интервала амплитуда остаётся постоянной, но меняется случайным образом от интервала к интервалу. Если считать что плотность распределения амплитуды подчиняется закону Рэлея, то вероятность ошибки
где На рисунке показана зависимость
Здесь же для сравнения приведена кривая, характеризующая потенциальную помехоустойчивость той же системы при когерентном приёме (кривая 1). Сравнение кривых показывает, что для рассматриваемой системы связи (с равными энергиями, ортогональной в усиленном смысле) априорное знание фазы и когерентный приём дают лишь очень небольшой энергетический выигрыш по сравнению со случаем некогерентного приёма. Этот выигрыш тем меньше, чем ниже допустимая вероятность ошибки. Для каналов с замиранием вероятность ошибки увеличивается и может быть снижена за счёт увеличения мощности сигнала. Систему ФМн так же как и другие системы с противоположными сигналами, отличающимися сдвигом фаз на
|

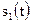 и
и  , полагая, что априорные вероятности этих сигналов одинаковы. Приходящий сигнал Z(t) является случайным, так как, во-первых, заранее неизвестна реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N(t).
, полагая, что априорные вероятности этих сигналов одинаковы. Приходящий сигнал Z(t) является случайным, так как, во-первых, заранее неизвестна реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N(t). (3.36)
(3.36) . При этом вероятность ошибки
. При этом вероятность ошибки 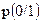 определится вероятностью того, что неравенство (13.36) не выполнено. Заметим z(t) и E их значениями:
определится вероятностью того, что неравенство (13.36) не выполнено. Заметим z(t) и E их значениями: , (3.37)
, (3.37)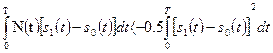 (3.38)
(3.38)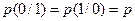 и сформированный модемом двоичный дискретный канал симметричен.
и сформированный модемом двоичный дискретный канал симметричен.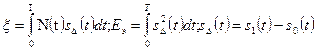 (3.39)
(3.39)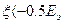 (3.40)
(3.40) , то
, то  – нормально распределённая величина, так как она определяется линейной операцией над нормальным же случайным процессом.
– нормально распределённая величина, так как она определяется линейной операцией над нормальным же случайным процессом. – функции, можем получить дисперсию величины
– функции, можем получить дисперсию величины  (3.41)
(3.41)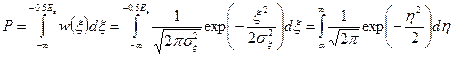 (3.42)
(3.42)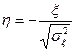 и введено обозначение
и введено обозначение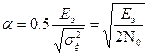 (3.43)
(3.43)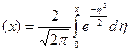 – табулирована и называется функцией Крампа. Учитывая, что
– табулирована и называется функцией Крампа. Учитывая, что 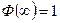 можно (3.42) записать в виде
можно (3.42) записать в виде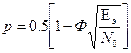 (3.44)
(3.44)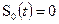 ;
; 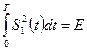 ;
; 

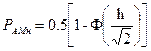 (3.45)
(3.45)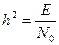 – отношение энергии сигнала на входе демодулятора к спектральной плотности флуктуационной помехи.
– отношение энергии сигнала на входе демодулятора к спектральной плотности флуктуационной помехи. (3.46)
(3.46)
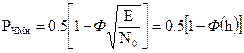 (3.46)
(3.46)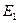 и
и 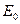 получатся, если
получатся, если 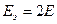
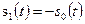

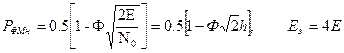 (3.47)
(3.47) и
и  передаются с одинаковой вероятностью).
передаются с одинаковой вероятностью). . Поэтому реальная помехоустойчивость при ЧМн близка к потенциальной, АМн значительно ниже её.
. Поэтому реальная помехоустойчивость при ЧМн близка к потенциальной, АМн значительно ниже её.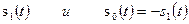 передаются равновероятно, то спектр сигнала ФМн вообще не содержит составляющей на частоте
передаются равновероятно, то спектр сигнала ФМн вообще не содержит составляющей на частоте 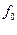 .
.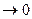 ). Возникает явление «обратной работы». Поэтому внедрение систем с ФМн долгое время реально было невозможным.
). Возникает явление «обратной работы». Поэтому внедрение систем с ФМн долгое время реально было невозможным.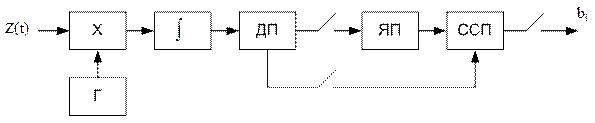
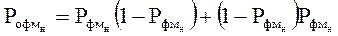 .
.

 (3.48)
(3.48)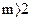 ) нахождение вероятности ошибочного приёма
) нахождение вероятности ошибочного приёма  в общем случае затрудняется, так как приходится анализировать совокупность из (m-1) неравенств. Однако для систем с активной паузой (
в общем случае затрудняется, так как приходится анализировать совокупность из (m-1) неравенств. Однако для систем с активной паузой (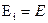 ) при равновероятных ортогональных сигналах канал симметричен и можно оценить вероятность
) при равновероятных ортогональных сигналах канал симметричен и можно оценить вероятность 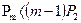 , (3.49)
, (3.49)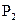 – вероятность ошибки для двоичной системы в том же канале, если используется некоторая пара из m сигналов.
– вероятность ошибки для двоичной системы в том же канале, если используется некоторая пара из m сигналов. . Такой метод приёма называется некогерентным. Для вывода правила оптимального некогерентного приёма воспользуемся критерием максимального правдоподобия. Математическая модель такого канала:
. Такой метод приёма называется некогерентным. Для вывода правила оптимального некогерентного приёма воспользуемся критерием максимального правдоподобия. Математическая модель такого канала: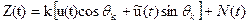 (3.50)
(3.50)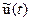 – преобразование Гильберта от U(t),
– преобразование Гильберта от U(t), 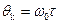 – случайная начальная фаза, k– коэффициент передачи канала.
– случайная начальная фаза, k– коэффициент передачи канала.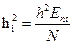
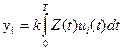
 (3.51)
(3.51) (3.52)
(3.52)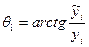 (3.53)
(3.53)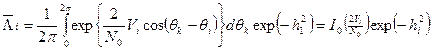 , (3.54)
, (3.54) - модифицированная функция Бесселя.
- модифицированная функция Бесселя.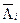 можно сравнить их логарифмы, что приводит к следующему алгоритму, который для двоичной системы будет выглядеть:
можно сравнить их логарифмы, что приводит к следующему алгоритму, который для двоичной системы будет выглядеть: (3.56)
(3.56)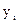 и
и  можно получить в момент отсчёта Т на выходе активного фильтра с опорными сигналами, равными соответственно
можно получить в момент отсчёта Т на выходе активного фильтра с опорными сигналами, равными соответственно 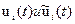 . С учётом сказанного можно осуществить построение на основе активных фильтров схемы, называемой квадратурной и реализующей алгоритм (3.56).
. С учётом сказанного можно осуществить построение на основе активных фильтров схемы, называемой квадратурной и реализующей алгоритм (3.56).
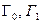 – соответственно генераторы опорных сигналов
– соответственно генераторы опорных сигналов 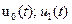 ; 90 градусов – фазовращатель всех сигнальных компонентов на 90 градусов (преобразователь Гильберта); БОМ – блок определения модуля вектора
; 90 градусов – фазовращатель всех сигнальных компонентов на 90 градусов (преобразователь Гильберта); БОМ – блок определения модуля вектора  ; НУ – нелинейные безынерционные устройства с характеристикой.
; НУ – нелинейные безынерционные устройства с характеристикой.  (3.57)
(3.57)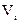 не зависят от начальной фазы сигналов
не зависят от начальной фазы сигналов  и пропорциональны огибающей (в моменты отсчёта, кратные Т) на выходе фильтра, согласованного с сигналом
и пропорциональны огибающей (в моменты отсчёта, кратные Т) на выходе фильтра, согласованного с сигналом 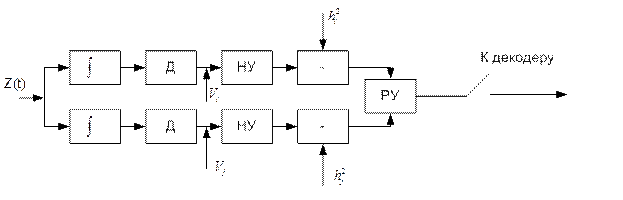 Идеальный детектор Д выделяет огибающую напряжения на выходе согласованного фильтра.
Идеальный детектор Д выделяет огибающую напряжения на выходе согласованного фильтра.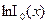 алгоритм оптимального некогерентного приёма можно записать так:
алгоритм оптимального некогерентного приёма можно записать так: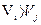
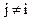
 (3.58)
(3.58)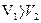 (3.59)
(3.59)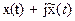 и
и  также ортогональны. Определим вероятность ошибки при приёме по алгоритму (3.59) двоичных сигналов, удовлетворяющих условиям ортогональности в усиленном смысле. Если передаётся символ 1, то с учётом (3.11) и (3.59) имеем:
также ортогональны. Определим вероятность ошибки при приёме по алгоритму (3.59) двоичных сигналов, удовлетворяющих условиям ортогональности в усиленном смысле. Если передаётся символ 1, то с учётом (3.11) и (3.59) имеем: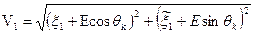 (3.60)
(3.60)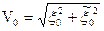 , где (3.61)
, где (3.61)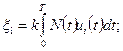

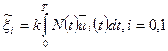 (3.62)
(3.62) , то
, то  и
и  при системе сигналов, ортогональной в усиленном смысле, равны нулю. Некоррелированность гауссовских величин означает их независимость. Следовательно, случайные величины
при системе сигналов, ортогональной в усиленном смысле, равны нулю. Некоррелированность гауссовских величин означает их независимость. Следовательно, случайные величины  и
и 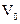 независимы, причём
независимы, причём  (3.63)
(3.63) (3.64)
(3.64) (3.65)
(3.65) – для системы ортогональных сигналов в усиленном смысле (ЧМн) (3.66)
– для системы ортогональных сигналов в усиленном смысле (ЧМн) (3.66)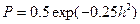 (3.67)
(3.67)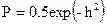 (3.68)
(3.68)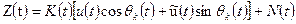
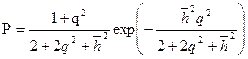 (3.69)
(3.69)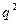 – отношение мощностей постоянной и флуктуирующей составляющих.
– отношение мощностей постоянной и флуктуирующей составляющих. согласно (3.66) в двоичной системе, ортогональной в усиленном смысле, с равными энергиями, например ЧМн при оптимальном некогерентном приёме (кривая 2), а также зависимость
согласно (3.66) в двоичной системе, ортогональной в усиленном смысле, с равными энергиями, например ЧМн при оптимальном некогерентном приёме (кривая 2), а также зависимость 
 , при некогерентном приёме применять нельзя, так как при неизвестной начальной фазе такие сигналы неразличимы. Однако, если сдвиг фазы в канале изменяется достаточно медленно, то разности фаз между соседними элементами практически сохраняются и могут быть измерены в приёмнике. Поэтому вполне возможен некогерентный приём при ОФМн.
, при некогерентном приёме применять нельзя, так как при неизвестной начальной фазе такие сигналы неразличимы. Однако, если сдвиг фазы в канале изменяется достаточно медленно, то разности фаз между соседними элементами практически сохраняются и могут быть измерены в приёмнике. Поэтому вполне возможен некогерентный приём при ОФМн.


