Элементы теории решений
Пусть при передаче дискретных сообщений, закодированных кодом с основанием m используются реализации сигнала передавался кодовый символ …………………………. передавался кодовый символ
Для двоичной системы (m=2) приёмное устройство выбирает одну из двух альтернативных гипотез о передаче символа 1 или 0. Совокупность всех возможных реализаций Z(t) можно интерпретировать точками в пространстве Z принимаемых сигналов. Будем графически изображать реализации принимаемых сигналов В математической теории связи это разбиение называют решающей схемой. В некоторых случаях пользуются решающей схемой со стиранием, или отказом от решения. Это значит, что m областей не охватывают всего пространства сигналов Z, и если приходящий сигнал не попадает ни в одну из этих областей, то принимается решение о стирании либо о невозможности определить передаваемый символ. В двоичной системе пространство Z разбивают на две непересекающиеся области
где Если помехи отсутствуют, возможные значения Например, если в разбиении, показанном на рисунке расширить область Осуществить наилучшее разбиение пространства принимаемых сигналов методами теории статистических решений (оптимизацию решающей схемы приёмного устройства) можно, если задан критерий качества. 3.3. Критерии качества оптимального приёмника
I.Критерий идеального наблюдателя, или критерий Котельникова Это критерий, по которому качество приёмника оценивают безусловной вероятностью правильного приёма сигнала. Пусть на вход приёмника в течение тактового интервала 0-Т приходит некоторый элемент сигнала Z(t). Предположим, что приёмник принимает при этом решение, что передан символ Очевидно, что вероятность правильного приёма будет максимальной в такой решающей схеме, для которой апостериорная вероятность
Согласно известной формуле Бейеса для
где Подставив (3.4) в (3.3) и учитывая, что
где Для построения решающей схемы по правилу (3.5) необходимо знать априорные вероятности символов Недостатком критерия максимума апостериорной вероятности является тот факт, что он обеспечивает большую вероятность правильного приёма за счёт сокращения области маловероятных и расширения области приёма высоковероятных символов; в результате редко передаваемые символы передавались бы менее надёжно, а они несут больше информации. II. Правило (3.5) можно записать иначе- решение о том, что передавался символ
Отношение в левой части этого неравенства называется отношением правдоподобия двух гипотез о том, что передавался символ Для двоичной системы правило сводится к проверке
Во многих случаях различные ошибки приводят к различным последствиям. III. Учёт последствий ошибок различного рода (связанных с передачей различных символов приводит к обобщению критерия идеального наблюдателя, известного под названием критерия минимального среднего риска (или байесовского критерия). Если при передаче символа Чтобы учесть неравноценность различных ошибок, будем с каждой парой символов Так как при передаче символа
Интервал берётся по области
Критерий минимального среднего риска заключается в том, что оптимальной считается решающая схема, обеспечивающая наименьшее значение среднего риска IV Ситуация, в которой практически невозможно определить априорную вероятность передачи отдельных элементарных сообщений, а последствия ошибок разного рода неодинаковы, особенно типична для радиолокации, когда приёмник, анализируя принимаемое колебание Z(t) (отражённый сигнал плюс помеха), должен определить, имеется в данном направлении и на данном расстоянии объект наблюдения (цель) или нет. Последствия двух родов ошибок ложной тревоги и пропуска цели – неравноценны. В этой и других сходных ситуациях чаще всего пользуются критерием приёма, известным под названием критерия Неймана Пирсона. Суть его заключается в том, что решающая схема считается оптимальной, если при заданной вероятности ложной тревоги Введём в рассмотрение функции правдоподобия гипотезы об отсутствии цели w(Z/0) и о наличии цели w(Z/1). Минимизация
Где
В технике связи преимущественно применяют правило максимального правдоподобия. В том случае, когда все символы передаются равновероятно, правило максимального правдоподобия переходит в критерий идеального наблюдателя. Часто это правило решения применяют и при неизвестных или известных но не одинаковых априорных вероятностях символов. Правило максимального правдоподобия переходит в критерий минимума среднего риска, если положить Существуют так же и другие критерии, например, критерий взвешенной вероятности ошибки, минимаксный критерий, при котором коэффициент потерь считается заданным и другие. Выбор того или иного варианта критерия оптимальности называют стратегией. Стратегия определяется исходными данными при проектировании. Наиболее простая стратегия соответствует критерию максимального правдоподобия. Рассматриваемые задачи в статистической теории связи классифицируются как задачи распознавания и задачи обнаружения сигнала. Например, при амплитудной телеграфии (АТ) – передача с «пассивной паузой» - приёмное устройство выполняет функции обнаружителя. (Термин «обнаружение» первоначально возник в радиолокации). В случае частотной или фазовой телеграфии (ЧТ или ФТ) приёмное устройство работает по принципу распознавания.
3.4 Алгоритм оптимального приёма при полностью известных сигналах. Когерентный приём
Полностью известными называются сигналы, у которых известны информационные параметры (то есть параметры, которые модулируются). Когерентный приём – это приём полностью известных сигналов. Предположим, что в канале действует наиболее типичная помеха – гауссовский аддитивный шум N(t), который в начале будем считать белым (широкополосным) со спектральной плотностью
где все Будем так же считать, что все сигналы Определим в этих условиях алгоритм работы оптимального приёмника, анализирующего сигнал на тактовом интервале 0-Т по критерию максимального правдоподобия. Алгоритм предусматривает ряд отдельных последовательных действий – «шагов» 1) Примем так называемую нулевую (или шумовую) гипотезу: S(t)=0; Z(t)=N(t) То есть предположим, что на вход приёмника поступает только шум.
3) Возьмём на тактовом интервале (Т) n равноотстоящих сечений через 4) Поэтому n-мерная плотность вероятностей для взятых отсчётов:
где 5) При гипотезе, что передавался символ
6) Отношение правдоподобия для сигнала
(3.14) 7) Заменим дисперсию Тогда
8) По правилу максимума правдоподобия в случае квазибелого шума решающая схема должна выбирать значение i, обеспечивающее максимум
9) Второй член в (3.16) можно при сравнении гипотез не учитывать, он сокращается. Тогда правило решения о том, что передавался символ
10) Вернёмся теперь к исходной задаче для белого шума. Для этого будем расширять полосу F, тогда число сечений n стремится к бесконечности,
Выражение (3.18) определяет те операции (алгоритм работы), которые должен совершать оптимальный приёмник над входным колебанием Z(t).
3.5 Структурное построение оптимального приёмника
Структурная схема приёмного устройства, работающего в соответствии с алгоритмом (3.18) для m=2
Здесь «–» - вычитающие устройства;
«Кв» - квадраторы;
РУ – решающее устройство, определяющее в момент времени, кратные Т (при замыкании ключей), номер ветви с минимальным сигналом. При m> 2 в схеме растёт соответственно число ветвей обработки сигнала, попадающих на РУ. Наличие в схеме квадраторов, призванных обеспечить квадратичное преобразование мгновенных значений входных сигналов во всём их динамическом диапазоне, часто затрудняет её реализацию. Поэтому на основе (3.18) получим эквивалентный алгоритм приёма, не требующий устройств возведения в квадрат. Раскрыв скобки под знаком интеграла и сократив в обеих частях неравенств (3.18) слагаемое
где
Для двоичной системы алгоритм (13.20) сводится к проверке одного неравенства:
Устройство, непосредственно вычисляющее скалярное произведение
называют активным фильтром или коррелятором; поэтому приёмник, реализующий алгоритм (3.22), называют корреляционным.
Если сигналы
Из (3.24) видно, что правило решения не изменится, если сигнал z(t), поступающий на вход демодулятора, умножить на любое число. Поэтому система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приёма в ней не требует знания «масштаба» приходящего сигнала или, другими словами, знания коэффициента передачи k канала. Эта важная особенность обусловила широкое распространение систем сигналов с равной энергией, которые обычно называют системами с активной паузой. Это особенно важно для каналов с замираниями, в которых коэффициент передачи флуктуирует. Для двоичной системы неравенство (3.22) можно представить в более простом виде:
где Существуют также системы с пассивной паузой. Реализуем алгоритм (3.25) для двоичной системы передачи однополярными импульсами (с пассивной паузой):
Рассмотренную систему двоичных сигналов используют в простейших устройствах проводной связи. В радиоустройствах, а также в современных кабельных каналах связи применяют высокочастотные сигналы. Наиболее простыми двоичными системами с гармоническими сигналами являются системы с амплитудой (АМ), фазовой (ФМ) и частотной (ЧМ) манипуляцией. В двоичной АМ
Оно реализуется схемой с блоком перемножения приходящего сигнала с опорным сигналом При двоичной ФМ системе Это – система с активной паузой, и поэтому в (3.25)
3.6 Реализация алгоритма оптимального приёма на основе согласованных фильтров. Свойства согласованного фильтра
Скалярное произведение (3.23) можно вычислить не только с помощью активного фильтра (коррелятора), но и с помощью пассивного линейного фильтра с постоянными параметрами. Если на вход фильтра подать принимаемый сигнал z(t), то напряжение на выходе фильтра можно выразить:
Такой фильтр называется согласованным с сигналом
Свойства согласованного фильтра: 1. Функция h(t) является зеркальным отображением s(t) относительно оси, проведённой через точку
2. Если финитный сигнал S(t) поступает на вход согласованного фильтра в момент t=0 и заканчивается в момент Т, условие физической реализуемости согласованного фильтра заведомо выполняется, если момент отсчёта – постоянная
3. Передаточная функция согласованного фильтра с импульсной реакцией (3.28)
где 4.Если на вход фильтра подан сигнал, с которым он согласован, то сигнальная составляющая на выходе согласованного фильтра
где Согласно (3.27) в момент времени Т напряжение на выходе согласованного фильтра пропорционально сигналу на выходе интегратора активного фильтра. Поэтому оптимальный приёмник, реализующий алгоритм (3.22), может быть выполнен и на базе согласованных фильтров. Структурная схема такого приёмника для двоичной системы показана на рисунке
Рассмотрим ещё одно важное свойство согласованного фильтра. Будем подавать сумму детерминированного сигнала и белого шума z(t)=s(t)+N(t) на вход различных линейных цепей с постоянными параметрами и измерять в момент Пусть
Мощность шума (дисперсия) на выходе цепи Согласно неравенству Коши Буняковского-Шварца для любых комплексных функций A(x) и B(x) при
причём равенство имеет место только при B(x)=aA(x) (3.33), где a – произвольная постоянная. Применим неравенство Бунявского-Шварца к числителю (3.33). Если положить:
то получим,
где Знак равенства согласно (3.34) и (3.35) имеет место тогда, когда передаточная функция удовлетворяет (3.30), то есть для согласованного фильтра, что и требовалось доказать. ( Рассмотрим возможности реализации согласованных фильтров. Согласованный фильтр для финитного сигнала произвольного вида s(t) можно, в принципе, построить на основе неискажающей длинной линии, обеспечивающей задержку сигнала на время Т, с бесконечной плотностью отводов, расположенных в дискретных точках с разносом
Если на вход А линии в начальный момент подаётся один короткий единичный импульс, аппроксимирующий Существуют различные другие способы реализации фильтра, точно или приближённо согласованного с сигналом заданной формы. Так, например, фильтр, согласованный с прямоугольным импульсом длительностью Т, который по определению должен иметь импульсную реакцию также в форме прямоугольного импульса, можно построить по схеме,
содержащей конденсатор, линию задержки на время Т, инвертор и сумматор. Если на вход этого фильтра подать единичный импульс (дельта - функцию), то он зарядит конденсатор до некоторого напряжения. Затем спустя время Т через линию задержки и инвертор такой же входной импульс противоположной полярности поступит на конденсатор и разрядит его. Как следствие, на выходе фильтра образуется в качестве импульсной реакции прямоугольный импульс. Вариант фильтра, согласованного с прямоугольным радиоимпульсом
Сравним реализации на активных фильтрах и СФ. 1. Схема с согласованными фильтрами на первый взгляд кажется проще схемы с активными фильтрами, поскольку в ней нет опорных генераторов и не возникает проблемы обеспечения их когерентности (согласование по фазе с приходящим сигналом). Однако и в схеме с согласованными фильтрами имеются свои практические трудности. В этом можно убедится, сравнив эпюры напряжений (без учёта помех в канале) на выходе фильтра (рис. Б), согласованного с прямоугольным радиоимпульсом (рис.А) и на выходе интегратора активного фильтра (рис.В).
Отметим, что всюду, за исключением точки t=T, напряжения на выходах обоих фильтров отличаются друг от друга. Из рисунков видно, что допустимая неточность во времени 2. В приёмниках на корреляторах легче осуществить переход на другую частоту. (В случае с СФ – нужно строить новый СФ). Иногда в технике связи используют фильтры, характеристики которых только частично согласованы с характеристиками сигнала. Такие фильтры называются квазиоптимальными.
|

 , 0< t< T, соответствующие кодовым символам
, 0< t< T, соответствующие кодовым символам  . В течение тактового интервала 0< t< T на вход приёмного устройства поступает колебание Z(t), которое вследствие искажений и помех в канале, не совпадает в точности не с одним из сигналов
. В течение тактового интервала 0< t< T на вход приёмного устройства поступает колебание Z(t), которое вследствие искажений и помех в канале, не совпадает в точности не с одним из сигналов  , то есть сигнал
, то есть сигнал  .
. , то есть сигнал
, то есть сигнал  .
.
 и помехи n(t) длительностью Т точками на плоскости или соответствующими векторами, откладываемыми от начала координат 0. Если правило решения выбрано, то это означает, что каждой точке пространства принимаемых колебаний (концу вектора) Z=S+n приписывается одна из m гипотез, то есть определённый передаваемый кодовый символ
и помехи n(t) длительностью Т точками на плоскости или соответствующими векторами, откладываемыми от начала координат 0. Если правило решения выбрано, то это означает, что каждой точке пространства принимаемых колебаний (концу вектора) Z=S+n приписывается одна из m гипотез, то есть определённый передаваемый кодовый символ 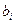 . Пространство принимаемых сигналов окажется при этом разбитым на m непересекающихся областей
. Пространство принимаемых сигналов окажется при этом разбитым на m непересекающихся областей 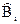 , каждая из которых соответствует принятию определённой гипотезы. В такой трактовке различные приёмные устройства отличаются друг от друга способом разбииения пространства сигналов на области
, каждая из которых соответствует принятию определённой гипотезы. В такой трактовке различные приёмные устройства отличаются друг от друга способом разбииения пространства сигналов на области  и
и 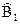 . Пусть на интервале 0-Т принимается колебание
. Пусть на интервале 0-Т принимается колебание (3.2)
(3.2) – полезный сигнал в месте приёма, прошедший канал связи, а n(t) – реализация аддитивной помехи.
– полезный сигнал в месте приёма, прошедший канал связи, а n(t) – реализация аддитивной помехи. изображаются точками
изображаются точками  . При наличии помехи и передаче сигнала с номером i точка принимаемого колебания Z отклоняется от точки
. При наличии помехи и передаче сигнала с номером i точка принимаемого колебания Z отклоняется от точки  . На рис. это показано для сигналов
. На рис. это показано для сигналов  ,
,  . Обычно область
. Обычно область  , то уменьшится вероятность, ошибочного приёма символа
, то уменьшится вероятность, ошибочного приёма символа 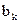 , вместо предаваемого символа
, вместо предаваемого символа  . Однако в этом случае возрастает вероятность ошибочного приёма передаваемого
. Однако в этом случае возрастает вероятность ошибочного приёма передаваемого  . Её называют обычно апостериорной вероятностью символа
. Её называют обычно апостериорной вероятностью символа  (3.3)
(3.3) (3.4)
(3.4) – n-мерная плотность вероятности вектора Z,
– n-мерная плотность вероятности вектора Z,  – априорная вероятность передачи символа
– априорная вероятность передачи символа  , (3.5)
, (3.5) – функция правдоподобия i -той гипотезы
– функция правдоподобия i -той гипотезы , определяемые источником, а также свойства модулятора и канала, определяющие условные плотности вероятности.
, определяемые источником, а также свойства модулятора и канала, определяющие условные плотности вероятности. 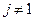 выполняется m-1 неравенств:
выполняется m-1 неравенств: (3.6)
(3.6) .
. (3.7)
(3.7) , то при
, то при  и
и 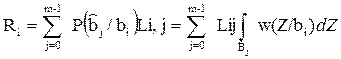 (3.8)
(3.8) решающей схемы и представляет вероятность того, что сигнал Z(t) попал в эту область, если передавался символ
решающей схемы и представляет вероятность того, что сигнал Z(t) попал в эту область, если передавался символ  по всем символам
по всем символам 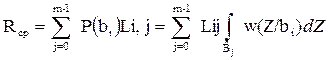 (3.9)
(3.9) . Приёмник, работающий по такому критерию называется байесовским. Из (3.9) видно, что при использовании этого критерия нужно помимо априорных вероятностей
. Приёмник, работающий по такому критерию называется байесовским. Из (3.9) видно, что при использовании этого критерия нужно помимо априорных вероятностей  ), то критерий минимального среднего риска совпадает с критерием идеального наблюдателя, а байесовский приёмник совпадает с идеальным приёмником Котельникова.
), то критерий минимального среднего риска совпадает с критерием идеального наблюдателя, а байесовский приёмник совпадает с идеальным приёмником Котельникова. обеспечивается минимальная вероятность пропуска цели
обеспечивается минимальная вероятность пропуска цели  .
.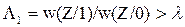 (3.10)
(3.10) – пороговый уровень, определяемый заданной вероятностью ложной тревоги
– пороговый уровень, определяемый заданной вероятностью ложной тревоги  .
. . Это значит, что при передаче сигнала
. Это значит, что при передаче сигнала  (символа
(символа  (3.11)
(3.11) известны. Неизвестны лишь реализация помехи и индекс i действительно переданного сигнала, который и должна определить решающая схема.
известны. Неизвестны лишь реализация помехи и индекс i действительно переданного сигнала, который и должна определить решающая схема. 2) Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечное. Для таких сигналов не существует плотности вероятностей. Однако существуют n-мерные плотности вероятностей для любых n сечений сигнала. Поэтому заменим белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности
2) Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечное. Для таких сигналов не существует плотности вероятностей. Однако существуют n-мерные плотности вероятностей для любых n сечений сигнала. Поэтому заменим белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности  , но только в некоторой полосе частот F.
, но только в некоторой полосе частот F. . Отсчёты
. Отсчёты  в этих сечениях квазибелого гауссовского шума независимы.
в этих сечениях квазибелого гауссовского шума независимы. (3.12)
(3.12)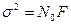 – дисперсия (мощность) квазибелого шума.
– дисперсия (мощность) квазибелого шума. , согласно (3.11)
, согласно (3.11)  . Следовательно, условная n-мерная плотность вероятности сечений Z(t) определяется такой же формулой, как и (3.12), если
. Следовательно, условная n-мерная плотность вероятности сечений Z(t) определяется такой же формулой, как и (3.12), если 
 , представляющей при этой гипотезе шум:
, представляющей при этой гипотезе шум: (3.13)
(3.13) (относительно дополнительной гипотезы), вычисленное для n сечений:
(относительно дополнительной гипотезы), вычисленное для n сечений:
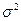 её выражением
её выражением 
 (3.15)
(3.15) . Вместо максимума
. Вместо максимума  можно отыскивать максимум его логарифма:
можно отыскивать максимум его логарифма: (3.16)
(3.16) (3.17)
(3.17) – к нулю. Суммы в (3.17) обратятся в интегралы, и правило решения определяется так:
– к нулю. Суммы в (3.17) обратятся в интегралы, и правило решения определяется так: (3.18)
(3.18)
 – генераторы опорных сигналов
– генераторы опорных сигналов  ;
; – интегралы;
– интегралы; , приходим к алгоритму приёма:
, приходим к алгоритму приёма: (3.19)
(3.19) – энергии ожидаемого сигнала
– энергии ожидаемого сигнала 
 (3.20)
(3.20) (3.22)
(3.22) (3.23)
(3.23) На рисунке показана структурная схема приёмного устройства, работающего в соответствии с (3.22). Здесь блоки x – перемножители;
На рисунке показана структурная схема приёмного устройства, работающего в соответствии с (3.22). Здесь блоки x – перемножители;  – генераторы опорных сигналов
– генераторы опорных сигналов  – интеграторы; «–» - вычитающие устройства; РУ – решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключа), i=0, 1 – номер ветви с максимальным сигналом.
– интеграторы; «–» - вычитающие устройства; РУ – решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключа), i=0, 1 – номер ветви с максимальным сигналом. выбраны таким образом, что все их реализации (а следовательно, и все реализации
выбраны таким образом, что все их реализации (а следовательно, и все реализации  ) имеют одинаковые энергии (
) имеют одинаковые энергии (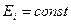 ), алгоритм приёма (3.22) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид:
), алгоритм приёма (3.22) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид: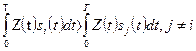 (3.24)
(3.24) , (3.25)
, (3.25)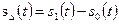 – разностный сигнал;
– разностный сигнал;  – пороговый уровень. Для системы с активной паузой
– пороговый уровень. Для системы с активной паузой 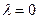 , что значительно облегчает реализацию оптимальной схемы.
, что значительно облегчает реализацию оптимальной схемы. . При этих сигналах
. При этих сигналах 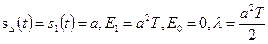 и (3.25) примет следующий вид:
и (3.25) примет следующий вид: (3.26)
(3.26) . Все входящие сюда постоянные (
. Все входящие сюда постоянные ( ) полагаем известными. Поскольку здесь
) полагаем известными. Поскольку здесь  , правило (3.26) запишется так:
, правило (3.26) запишется так:
 .
.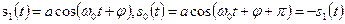
 – и реализуется той же схемой что двоичная АМ при
– и реализуется той же схемой что двоичная АМ при  . В этом случае решающее устройство играет роль дискриминатора полярностей.
. В этом случае решающее устройство играет роль дискриминатора полярностей. , где
, где  – импульсная реакция фильтра. Выберем её такой, чтобы в момент t=Т получить y(T), совпадающее со скалярным произведением (3.23). Легко видеть, что это будет выполнено, если
– импульсная реакция фильтра. Выберем её такой, чтобы в момент t=Т получить y(T), совпадающее со скалярным произведением (3.23). Легко видеть, что это будет выполнено, если 
 (3.27)
(3.27) . То есть фильтром, согласованным с сигналом
. То есть фильтром, согласованным с сигналом  , называется линейный фильтр с постоянными параметрами и импульсной реакцией:
, называется линейный фильтр с постоянными параметрами и импульсной реакцией: (3.28)
(3.28)

 удовлетворяет условию:
удовлетворяет условию: (3.29)
(3.29) , (3.30)
, (3.30) – функция комплексно-сопряжённая со спектральной плотностью сигнала s(t). Следовательно, АЧХ согласованного фильтра определяется амплитудным спектром сигнала s(t), а его ФЧХ (без учёта слагаемого –
– функция комплексно-сопряжённая со спектральной плотностью сигнала s(t). Следовательно, АЧХ согласованного фильтра определяется амплитудным спектром сигнала s(t), а его ФЧХ (без учёта слагаемого –  , определяемого задержкой
, определяемого задержкой  (3.31)
(3.31) – временная функция корреляции сигнала.
– временная функция корреляции сигнала.
 отношение мгновенной мощности сигнальной составляющей к средней мощности шума на выходе цепи. Докажем, что это отношение
отношение мгновенной мощности сигнальной составляющей к средней мощности шума на выходе цепи. Докажем, что это отношение  максимально, если цепь является согласованным фильтром.
максимально, если цепь является согласованным фильтром. – спектр входного сигнала, а
– спектр входного сигнала, а  – передаточная функция некоторой линейной цепи. Тогда спектр сигнальной составляющей
– передаточная функция некоторой линейной цепи. Тогда спектр сигнальной составляющей  на выходе цепи равен
на выходе цепи равен  . С помощью обратного преобразования Фурье найдём значение в момент
. С помощью обратного преобразования Фурье найдём значение в момент  (3.32)
(3.32) . Искомое отношение
. Искомое отношение  (3.33)
(3.33)
 , (3.34)
, (3.34) ,
, , (3.35)
, (3.35) – отношение энергии элемента сигнала Е на входе фильтра к спектральной плотности
– отношение энергии элемента сигнала Е на входе фильтра к спектральной плотности  белого шума.
белого шума.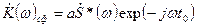 .)
.) , где F – эффективная ширина спектра сигнала.
, где F – эффективная ширина спектра сигнала.
 – функцию, то с отводов снимаются такие же импульсы, разнесённые на интервале
– функцию, то с отводов снимаются такие же импульсы, разнесённые на интервале  , которые пройдя через взвешивающие блоки
, которые пройдя через взвешивающие блоки  , поступают поочерёдно на вход ФНЧ. Взвешивающие блоки содержат усилители с коэффициентом усиления
, поступают поочерёдно на вход ФНЧ. Взвешивающие блоки содержат усилители с коэффициентом усиления  , а также при отрицательных
, а также при отрицательных 
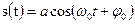 , заданном на интервале (0, T), показан ниже.
, заданном на интервале (0, T), показан ниже. Он состоит из идеального колебательного контура без потерь, настроенного на частоту
Он состоит из идеального колебательного контура без потерь, настроенного на частоту  и фазовращателя, сдвигающего фазу колебаний контура на –
и фазовращателя, сдвигающего фазу колебаний контура на –  . Линия задержки на Т в схеме и инвертор обеспечивают гашение колебаний фильтра вне интервала (0, T), импульсная же реакция фильтра на этом интервале с учётом фазовращателя
. Линия задержки на Т в схеме и инвертор обеспечивают гашение колебаний фильтра вне интервала (0, T), импульсная же реакция фильтра на этом интервале с учётом фазовращателя 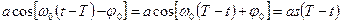 , что и обеспечивает согласование.
, что и обеспечивает согласование.



