Узкополосные сигналы
Сигнал называется узкополосным, если его спектральная плотность отлична от нуля лишь в пределах частотных интервалов шириной П, образующих окрестности точек Как правило, можно считать, что частота
Обе входящие функции Синфазную и квадратурную амплитуду можно выделить аппаратурным способом. Пусть имеется перемножающее устройство, на один из входов которого подан узкополосный сигнал
Пропустим выходной сигнал перемножителя через фильтр нижних частот (ФНЧ), подавляющий составляющие с частотами порядка Если на один из входов перемножителя подать вспомогательное колебание С физической точки зрения узкополосные сигналы представляют собой квазигармонические колебания. Обобщим метод комплексных амплитуд, известный из электротехники на узкополосные сигналы вида (3.18). Введём комплексную низкочастотную функцию:
называемую комплексной огибающей узкополосного сигнала. Формулу (3.19), определяющую комплексную огибающую, можно представить также в показательной форме:
Здесь Величины
Введём полную фазу узкополосного колебания
В соответствии с формулой (3.22) узкополосный сигнал общего вида представляет собой колебание, получающееся при одновременной модуляции несущего гармонического сигнала, как по амплитуде, так и по фазовому углу. Используя равенства (3.21) физическую огибающую
Комплексная огибающая узкополосного сигнала не определяется однозначно сигналом Если обозначить через
Таким образом, спектральная плотность узкополосного сигнала может быть найдена путём переноса спектра комплексной огибающей из окрестности нулевой частоты в окрестности точек Формула (3.25) полезна тем, что по известному спектру узкополосного сигнала позволяет найти спектр его комплексной огибающей, (которая в свою очередь определяет физическую огибающую и мгновенную частоту сигнала).
|

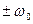 , причём должно выполняться условие
, причём должно выполняться условие 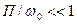 .
. , называемая опорной частотой сигнала, совпадает с центральной частотой спектра.
, называемая опорной частотой сигнала, совпадает с центральной частотой спектра. (3.18)
(3.18) и
и  является низкочастотными, их относительное изменение за период высокочастотных колебаний
является низкочастотными, их относительное изменение за период высокочастотных колебаний 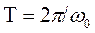 достаточно малы. Функцию
достаточно малы. Функцию 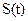 при заданном значении опорной частоты
при заданном значении опорной частоты 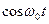 . На выходе перемножителя будет получен сигнал
. На выходе перемножителя будет получен сигнал  :
:
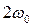 . Ясно, что с выхода фильтра будет поступать низкочастотное колебание, пропорциональное синфазной амплитуде
. Ясно, что с выхода фильтра будет поступать низкочастотное колебание, пропорциональное синфазной амплитуде 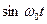 , то такая система будет выделять из узкополосного сигнала S(t) его квадратурную амплитуду
, то такая система будет выделять из узкополосного сигнала S(t) его квадратурную амплитуду 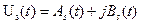 (3.19)
(3.19) (3.20)
(3.20)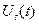 - вещественная неотрицательная функция времени, называемая физической огибающей (часто для практики просто огибающей),
- вещественная неотрицательная функция времени, называемая физической огибающей (часто для практики просто огибающей), 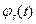 - медленно изменяющаяся во времени начальная фаза узкополосного сигнала.
- медленно изменяющаяся во времени начальная фаза узкополосного сигнала.
 (3.21) Откуда вытекает ещё одна форма записи математической модели узкополосного сигнала:
(3.21) Откуда вытекает ещё одна форма записи математической модели узкополосного сигнала: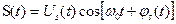 (3.22)
(3.22)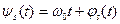 и определим мгновенную частоту сигнала, равную производной по времени от полной фазы:
и определим мгновенную частоту сигнала, равную производной по времени от полной фазы: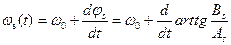 (3.23)
(3.23)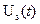 можно определить через синфазную и квадратурную амплитуды:
можно определить через синфазную и квадратурную амплитуды: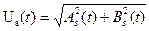 (3.24)
(3.24)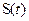 , а зависит также от выбора частоты
, а зависит также от выбора частоты 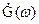 спектральную плотность комплексной огибающей узкополосного сигнала S(t); который, в свою очередь, имеет спектральную плотность
спектральную плотность комплексной огибающей узкополосного сигнала S(t); который, в свою очередь, имеет спектральную плотность 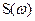 то нетрудно видеть что:
то нетрудно видеть что: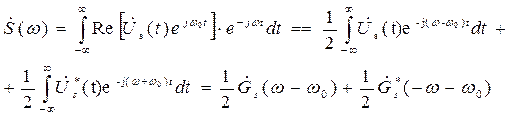 (3.25)
(3.25)


