Спектральные представления сигналов с использованием негармонических функций
Для представления непрерывных сигналов используются различные системы ортогональных функций. I. Для представления непрерывных сигналов используются преимущественно ортогональные функции и полиномы Лежандра, Чебышева, Лагерра и Эрмита.
1) Полиномы Лежандра (1-го рода) определяются формулой:
Ряд выглядит следующим образом:
Спектральные коэффициенты
2) Полиномы Чебышева (1-го рода) определяются формулой:
Ряд:

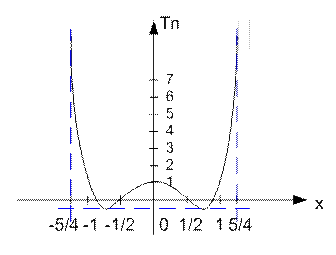
График полинома Чебышева 4-го порядка:
Полиномы Чебышева обеспечивают наименьшую максимальную ошибку аппроксимации на интервале
3) Полиномы Лагерра определяются формулой
Так как полиномы Лагерра образуют систему расходящихся при
Разложение в ряд по функциям Лагерра
коэффициенты должны определяться по формуле:
Функции Лагерра получили широкое распространение в измерительной технике и в многоканальных системах связи, что объясняется простотой их генерирования.
4) Полиномы Эрмита определяются формулой:
Разложение в ряд по нормированным функциям Эрмита:
Полиномы Эрмита отличаются от полиномов Лагерра тем, что полиномы Лагерра определены на интервале, представляющем собой полуось
II. Для представления дискретных сигналов используются в основном функции Уолша.
Чаще всего используются функции Уолша, которые на отрезке своего существования Введём безразмерное время Разложение сигнала в ряд по функциям Уолша на заданном отрезке времени имеет вид:
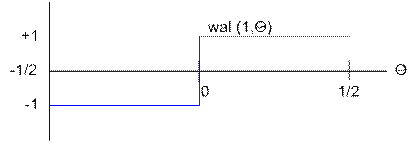
Графики функций Уолша
III. Вейвлет – анализ.
Если сигнал не имеет чёткого периодического характера, то алгоритмы преобразования Фурье становятся менее эффективными. Эта проблема в последние годы решается с помощью нового подхода в теории и технике сигналов – вейвлет–анализа. Wavelet – в переводе с английского “небольшая волна” или “небольшое колебание”.
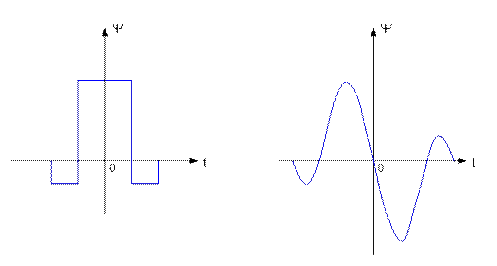
С помощью вейвлет–анализа можно представлять как дискретные, так и непрерывные сигналы. а) В основе дискретного вейвлет–анализа лежит использование исходного (или порождающего) вейвлета Хаара. Эта функция существует на отрезке [0, 1] и принимает одно из двух возможных значений.
Ортонормированная базисная система вейвлетов Хаара строится за счёт операций сдвига во времени и изменения временного масштаба. Тогда сигнал можно разложить в ряд по этим функциям, следующим образом:
На основании предыдущего, коэффициенты
Данный ряд отличается от изучавшегося ранее тем, что суммирование производится не по одному, а по двум индексам. Вейвлет – спектр сигнала, принимающего вещественные значения, можно образно представить себе как некоторый “лес” из вертикальных отрезков, размещенных над j k – плоскостью в точках с целочисленными координатами. При этом координата j указывает на скорость изменения сигнала, а координата k – на положение вдоль оси времени. б) Для анализа непрерывных сигналов пользуются непрерывными вейвлетами. Примером может служить вейвлет типа “сомбреро”:
Вейвлет–преобразованием
По своему смыслу вейвлет–преобразование соответствует преобразованию Фурье, только вместо функции Вейвлет–преобразование является функцией двух аргументов, первый из которых аналогичен периоду колебания (т.е. обратной частоте), а второй – смещению сигнала вдоль оси времени. Обратное вейвлет–преобразование:
Вейвлет–анализ особенно эффективен при решении задач сжатия и распознавания сигналов. Алгоритмы вейвлет–анализа представлены в составе прикладного пакета Mathlab. Раздел 3. Сигналы с ограниченным спектром
Для восстановления сигнала по его спектру необходимо учитывать все составляющие с частотами, лежащими в интервале от нуля до бесконечности. Однако с физической точки зрения такая процедура принципиально неосуществима. К тому же вклад спектральных составляющих при Поэтому на практике обычно используется математическая модель сигнала с ограниченным спектром. Сигналы, спектральная плотность которых отлична от нуля лишь в пределах некоторой полосы частот конечной протяжённости, называются сигналами с ограниченным спектром.
|

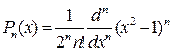 ,
, ,
, определяются формулой:
определяются формулой: ,
,



 функций, то удобнее пользоваться функциями Лагерра
функций, то удобнее пользоваться функциями Лагерра




 - коэффициенты ряда (спектральные составляющие)
- коэффициенты ряда (спектральные составляющие) , а полиномы Эрмита – на интервале, представляющем собой всю ось
, а полиномы Эрмита – на интервале, представляющем собой всю ось  .
. принимают лишь значения
принимают лишь значения  .
. , тогда k-ая функция Уолша обозначается символом
, тогда k-ая функция Уолша обозначается символом  .
.
 - коэффициенты ряда.
- коэффициенты ряда.


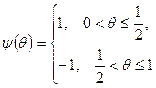
 - безразмерное время
- безразмерное время 
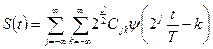
 являются скалярными произведениями исходного сигнала и соответствующей базисной функции:
являются скалярными произведениями исходного сигнала и соответствующей базисной функции:



 является функция двух переменных:
является функция двух переменных:
 используется вейвлет
используется вейвлет  .
.
 пренебрежимо мал в силу ограниченности энергии сигналов. Кроме того, любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.
пренебрежимо мал в силу ограниченности энергии сигналов. Кроме того, любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.


