Основы теории ортогональных сигналов
Введём понятие скалярного произведения элементов линейного пространства. Скалярное произведение вещественных сигналов u и v:
Скалярное произведение обладает следующими свойствами: 1. 2. 3. 4. 5. Линейное пространство с таким скалярным произведением, содержащее в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства называется вещественным Гильбертовым пространством H. Если сигналы принимают комплексные значения, то можно определить комплексное Гильбертово пространство. Если сигналы комплексные, то скалярное произведение:
Два сигнала
Предположим, что на отрезке
0, если Говорят, что при этом в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал
Такое представление называется обобщённым рядом Фурье сигнала Коэффициенты данного ряда находят следующим образом. Возьмём базисную функцию
Ввиду ортонормированности базиса по определению в правой части равенства (1.11) останется только член суммы с номером
Рассмотрим некоторый сигнал,
Поскольку базисная система функций ортонормирована, в сумме (1.13) отличными от нуля окажутся только члены с номерами
Смысл этой формулы: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщённый ряд Фурье.
Раздел 2. Спектральные представления сигналов
|

 (1.6)
(1.6)

 , где
, где  - вещественное число
- вещественное число
 - справедливо неравенство Коши-Буняковского.
- справедливо неравенство Коши-Буняковского. (1.7)
(1.7) и
и  называют ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:
называют ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю: (1.8)
(1.8) задана бесконечная система функций
задана бесконечная система функций  , ортогональных друг другу и обладающих единичными нормами:
, ортогональных друг другу и обладающих единичными нормами:
 1, если
1, если  (1.9)
(1.9)
 в ряд:
в ряд: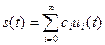 (1.10)
(1.10) с произвольным номером
с произвольным номером  , умножим на неё обе части равенства (1.10) и затем проинтегрируем результаты по времени:
, умножим на неё обе части равенства (1.10) и затем проинтегрируем результаты по времени: (1.11)
(1.11) , поэтому:
, поэтому: (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14)


