Некоторые математические модели сигналов с ограниченным спектром
1) Рассмотрим колебание с постоянной вещественной спектральной плотностью в пределах отрезка оси частот от
Мгновенное значение такого сигнала:
Спектральная плотность такого сигнала:
Такое колебание называется идеальным низкочастотным сигналом (ИНС). График ИНС, построенный по формуле (3.2) имеет вид осциллирующей кривой относительно отсчёта времени. С увеличением верхней граничной частоты спектра возрастают как центральный максимум, так и частота осцилляций.
ИНС более общего вида получается, если в формулу (3.1) ввести фазу спектральной плотности, линейно зависящую от частоты.
Спектральной плотности соответствует низкочастотный сигнал, смещённый во времени относительно сигнала (3.2) на
2) Исследуем математическую модель сигнала, спектр которого ограничен полосами частот шириной
По аналогии с предыдущим данный сигнал будем называть идеальным полосовым сигналом (ИПС). Мгновенные значения ИПС найдём, используя обратное преобразование Фурье:
Спектральная плотность ИПС:
Строя график ИПС, видим что наряду с высокочастотными осцилляциями на частоте
Теоретически возможный способ получения ИПС очевиден: на вход идеального полосового фильтра, пропускающего лишь колебания с частотами в пределах полосы Свойство ограниченности спектра позволяет находить интересные и важные классы ортогональных сигналов. Простейший пример – два ортогональных полосовых сигнала, области существования спектра которых не пересекаются. Менее очевидный способ ортогонализации сигналов с ограниченным спектром заключается в их временном сдвиге. Рассмотрим два идеальных низкочастотных сигнала
Скалярное произведение обращается в нуль и два одинаковых по форме ИНС оказываются ортогональными, если временной сдвиг удовлетворяет условию.
Минимально возможный сдвиг приводящий к ортогонализации, получается при
График двух идеальных низкочастотных сигналов:
В момент времени, когда один из сигналов достигает максимума, другие сигналы из данного семейства проходят через нуль.
|

 до верхней граничной частоты
до верхней граничной частоты  , вне этого отрезка спектральная плотность сигнала обращается в нуль:
, вне этого отрезка спектральная плотность сигнала обращается в нуль: (3.1)
(3.1) (3.2)
(3.2)

 (3.3)
(3.3) секунд.
секунд. (3.4) ИНС является идеализированной выходной реакцией фильтра низких частот (ФНЧ), возбуждаемого колебанием с равномерной по частоте спектральной плотностью, т.е. дельта-импульсом.
(3.4) ИНС является идеализированной выходной реакцией фильтра низких частот (ФНЧ), возбуждаемого колебанием с равномерной по частоте спектральной плотностью, т.е. дельта-импульсом. каждая с центрами на частотах
каждая с центрами на частотах  . Если в пределах этих полос спектральная плотность сигнала постоянна:
. Если в пределах этих полос спектральная плотность сигнала постоянна: (3.5)
(3.5) (3.6)
(3.6)
 наблюдается изменение во времени мгновенного значения их амплитуды. Функция
наблюдается изменение во времени мгновенного значения их амплитуды. Функция  с точностью до масштабного коэффициента
с точностью до масштабного коэффициента  играет роль медленной огибающей ИПС.
играет роль медленной огибающей ИПС.
 , должно быть подано широкополосное воздействие вида дельта-импульса.
, должно быть подано широкополосное воздействие вида дельта-импульса. и
и  . Оба этих сигнала имеют одинаковые параметры
. Оба этих сигнала имеют одинаковые параметры  и
и 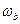 (см. формулу 3.2), однако сигнал
(см. формулу 3.2), однако сигнал  запаздывает по отношению к
запаздывает по отношению к  , так что его спектральная плотность
, так что его спектральная плотность  . Скалярное произведение этих сигналов, вычисленное через спектральные плотности.
. Скалярное произведение этих сигналов, вычисленное через спектральные плотности. (3.7)
(3.7)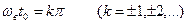
 :
: (3.8)
(3.8)



