Теорема Котельникова
Эта теорема (доказана академиком Котельниковым В.А. в 1933 г.), устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром, исходя из отсчетных значений (выборок), взятых через равные промежутки времени. Любые два сигнала с ограниченным спектром, принадлежащие семейству являются ортогональными если установить сдвиг Путём соответствующего выбора амплитудного множителя А можно добиться того, чтобы норма каждого из этих сигналов стала единичной. В результате будет построен ортонормированный базис, позволяющий разложить произвольный сигнал с ограниченным спектром в обобщённый ряд Фурье. Из семейства функции
так как норма любого сигнала
Функции
Бесконечная совокупность функций.
образует базис Котельникова в линейном пространстве низкочастотных сигналов со спектрами, ограниченными сверху значением
Коэффициентами ряда служат, как известно, скалярные произведения разлагаемого сигнала и k-той отсчётной функции:
Удобный способ вычисления этих коэффициентов заключается в применении теоремы Планшереля. Легко проверить, что каждая отсчётная функция в пределах отрезка Тогда, если Тогда:
Величина в фигурных скобках есть не что иное, как Таким образом:
Откуда следует выражение ряда Котельникова:
Теорему Котельникова принято формулировать так: произвольный сигнал, спектр которого не содержит частот выше Важная особенность теоремы Котельникова состоит в её конструктивном характере: она не только указывает на возможность разложения сигнала в соответствующий ряд, но и определяет способ восстановления непрерывного сигнала, заданного своими отсчётными значениями. Теорема Котельникова показывает возможность «цифровизации» непрерывных сообщений.
|

 (3.9)
(3.9)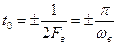
 достаточно рассмотреть лишь функцию
достаточно рассмотреть лишь функцию  при k=0.
при k=0. (3.10)
(3.10) одинакова независимо от сдвига во времени. Определим квадрат нормы
одинакова независимо от сдвига во времени. Определим квадрат нормы  и проинтегрируем по t.
и проинтегрируем по t.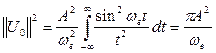
 (3.11)
(3.11) (3.12)
(3.12) . Отдельная функция
. Отдельная функция  произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот
произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот  то его можно разложить в обобщенный ряд Фурье по базису Котельникова:
то его можно разложить в обобщенный ряд Фурье по базису Котельникова: (3.13)
(3.13) (3.14)
(3.14) .
. - спектр излучаемого сигнала S(t), то по теореме Планшереля
- спектр излучаемого сигнала S(t), то по теореме Планшереля  ,
, (3.15)
(3.15) , т.е. мгновенное значение сигнала S(t) в каждой отсчётной точке
, т.е. мгновенное значение сигнала S(t) в каждой отсчётной точке 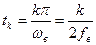 (по аналогии с
(по аналогии с 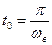 )
) (3.16)
(3.16) (3.17)
(3.17) Гц, может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени
Гц, может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени  с.
с.


