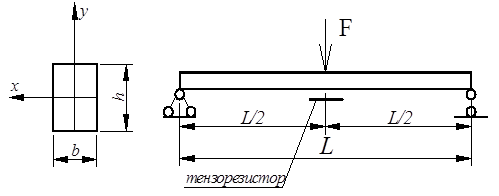
Задача №9. Определить величину нагрузки вызванный этой нагрузкой максимальный прогиб стальной балки, если измерена относительная деформация ε в крайнем нижнем
Определить величину нагрузки вызванный этой нагрузкой максимальный прогиб стальной балки, если измерена относительная деформация ε в крайнем нижнем волокне балки в сечении, где приложена сосредоточенная сила F (ε =80·10-5), модуль упругости стали Е =2, 1·105МПа.
Решение: Для однопролетной балки с шарнирным опиранием нагруженной сосредоточенной силой в середине пролета максимальные напряжения определяются из выражения:
Следовательно, нагрузка F может быть вычислена как:
В данном случае величина максимальных нормальных напряжений σ max определяется по закону Гука для одноосного напряженного состояния σ max=ε ·Е; Таким образом, значение F вычисляем по формуле:
Так как момент сопротивления прямоугольного сечения балки:
Окончательно величина нагрузки F будет равна:
Значение максимального прогиба для балки с шарнирным опиранием, нагруженной силой в середине пролета равно:
Величину момента инерции для прямоугольного сечения определяем по формуле:
Относительная величина максимального прогиба:
|


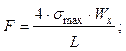

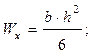




 .
.


