Проверочный расчет зубчатой передачи
5.1. Проверим межосевое расстояние: аw = (d1 + d2) /2 = (41, 03 + 198, 98) /2 = 120 (мм) 5.2. Проверим контактные напряжения
где K¢ – вспомогательный коэффициент. Для косозубых передач K¢ =376 (для прямозубых K=436); Ft = 2Т2 × 103 / d2 – окружная сила в зацеплении, Н для нашего случая, где Т2 = Т3 имеем, Ft = 2Т3 × 103 / d2= 2 × 0, 307 × 103 × 103/198, 98 = 3085, 7 Н. Кнa – коэффициент, учитывающий распределение нагрузки между зубьями: определяем по графику (рис. 5) в зависимости от окружной скорости колес ν = w3 d2 / (2 × 103), м/с и степени точности передачи (табл. 6): ν = 10, 23× 198, 98 / (2 × 103)= 1, 02 м/с. Принимаем, Кнa= 1, 11. Кнn – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (табл. 6) Кнn= 1, 01 Кнβ , Uф, d2, b2 – значения перечисленных величин определяли ранее (см. раздел 3, п.1, п.8, п.10, п.2). Подставим в формулу (36) полученные величины, имеем, что
Полученное значение контактного напряжения [s]н меньше допускаемого [sн] = 637, 9 МПа. Определим степень недо грузки по контактным напряжениям:
5.3. Проверим напряжение изгиба зубьев шестерни sF1 и колеса sF2, МПа:
где m – модуль зацепления, m = 4 мм по расчетам; Ft = 3085, 7 Н, окружная сила в зацеплении, по расчетам; КFa - коэффициент, учитывающий распределение нагрузки между зубьями, зависит для косозубых от степени точности передачи, определяемой по табл. 6, КFa = 1. Для прямозубых КFa = 1, задается. КFβ – коэффициент неравномерности нагрузки по длине зуба, выбираем аналогично КFβ , КFβ = 1; КFν - коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (см. табл. 7), КFν = 1, 04; УF1 и УF2 – коэффициенты формы зуба шестерни и колеса. Определяются по табл. 8 в зависимости от числа зубьев шестерни Z1 и колеса Z2 для прямозубых, а для косозубых - в зависимости от эквивалентного числа зубьев шестерни Zn1 =Z1/cosb и колеса Zn2=Z2/cosb, где β – угол наклона зубьев, определяемый ранее. Zn1 =Z1/cosb=20/cos (12, 84°)=20, 5=20. Zn2=Z2/cosb=97/cos (12, 84°)=99, 5=99. По табл.8 имеем: УF1 = 4, 07 УF2 = 3, 60. - Уβ = 1 - b° /140° - коэффициент, учитывающий наклон зуба, - Уβ = 1 – 12, 84°=/140° = 0, 91 - [s]F1 = 310 МПа и [s]F2 = 294 МПа – допускаемые напряжения изгиба шестерни и колеса, определены ранее (см. п.3, раздел 2) Подставим в формулу (37) и (38) известные величины и определим:
= 146 МПа sF1 = sF2 × УF1 / УF2 = 146 · 4, 07 / 3, 60 = 165, 1 МПа. Проверочный расчет показал, что расчетные значения sF значительно меньше [s]F, это допустимо, т.к. нагрузочная способность большинства зубчатых передач и рассматриваемого примера в частности, ограничивается контактной прочностью.
|

 н, Н/мм2:
н, Н/мм2: , (36)
, (36)
 (МПа).
(МПа). = 0, 92%.
= 0, 92%. , (37)
, (37)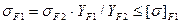 , (38)
, (38) = 36 мм, ширина венца зубчатого колеса, по расчетам;
= 36 мм, ширина венца зубчатого колеса, по расчетам;



