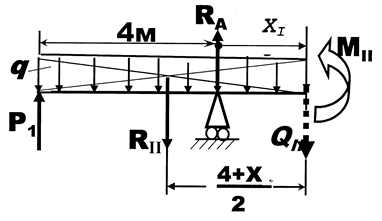
Построение эпюр поперечной силы Q и изгибающейго момента М
Рис. 3. Схема к построению эпюр Q и M Разбиваем балку на участки, для чего проводим границы участков через точки приложения сосредоточенных сил, сосредоточенных моментов, через начало и конец распределённой нагрузки. Таких границ оказывается пять, между ними расположено 4 участка. Делаем сечение I-I и рассматриваем равновесные части балки длиной «Х» левее этого сечения (рис.4). К этой части приложена сосредоточенная сила Р1 и часть распределенной нагрузки q лежащая на длине «Х» метров.
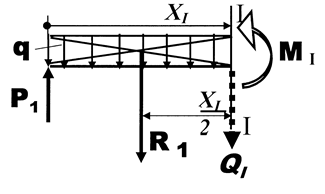 По сделанному сечению будут действовать внутренние силы, создающую поперечную (срезающую) силу Q1 и изгибающий момент MI. Составим уравнение статики для рассматриваемого участка. По сделанному сечению будут действовать внутренние силы, создающую поперечную (срезающую) силу Q1 и изгибающий момент MI. Составим уравнение статики для рассматриваемого участка.
Вместо равномерно распределенной нагрузки можно приложить в середине участка ееравнодействующую R1 равную произведению нагрузки приходящейся на 1 погонный метр (q) на длину участка на которой она приложена (X1) R=q × X1.
Из полученного можно сделать вывод, что поперечная сила Q численно равна алгебраической сумме внешних поперечных нагрузок (Р1 и R1) лежащих по одну сторону от сечения (I-I).Внешние поперечные нагрузки направленные вверх (Р1) входят в уравнение Q со знаком плюс, а вниз (R1) – со знаком минус Полученное уравнение для Q является прямолинейной зависимостью. Прямую строят по двум точкам. Значение X1 задаём в начале X1=0 и в конце участка Х1=4 м. X1=0; Q1=20-10 × 0=20(кН) Х1=4м; Q1=20-10 × 4=-20(кН) Для определения изгибающего момента в первом сечении MI составляем уравнение статики – сумму моментов относительно центра тяжести первого сечения.
Из полученного можно сделать вывод, что изгибающий момент М численно равен алгебраической сумме моментов от всех внешних нагрузок (Р1 и R1) лежащих по одну сторону от сечения (I-I).Моменты берутся относительно центра тяжести проведённого сечения. Внешние нагрузки действующие относительно центра тяжести проведённого сечения по часовой стрелке входят в уравнение М со знаком плюс, а против часовой стрелки со знаком минус. После подстановки значений Р1 и q получим:. MI=20х-5х2 уравнение параболы. При х=0 М=0; При х=4м М=20 × 4 – 5 × 42=0. Анализируем выражение изгибающего момента на экстремум
Вычисляем значения момента в сечении при х=2м. М=20 × 2-52=20 (кНм).
|


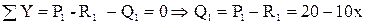

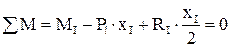 ;
; 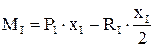
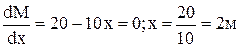 .
.