Расчет клиноременной передачи. 1. По табл. 9 с учетом полученного значения Т1 выбираем тип клинового ремня :
1. По табл. 9 с учетом полученного значения Т1 выбираем тип клинового ремня: Т1 = 0, 034 кН × м (см. раздел 1. п.6 «Кинематический расчет привода»). Согласно табл. 9 имеем тип клинового ремня А(А) нормального сечения (ГОСТ 1284.1 – 89; ГОСТ 1284.2 – 89) 2. Вычисляем диаметр ведущего шкива:
Из ряда стандартных значений: 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400, 450, 500, 560, 630, 710, 800, 900, 1000, 1120, 1250, 1400, 1600, 1800, 2000 мм выбираем d1 = 125 мм. Диаметр ведомого шкива определим по следующей зависимости: d2 = d1 × u (1 – ε), (44) где u – передаточное число открытой передачи, = 1, 907 (см. раздел 1, п.7 «Кинематический расчет привода»). ε – коэффициент скольжения 0, 08… 0, 02. Подставив в формулу 44 известные величины имеем, что d2 = d1 × u (1 – ε) = 125 × 1, 907 (1-0, 02) = 233, 5 = 234 мм. Из ряда стандартных значений принимаем d2 = 250 мм 3. Определяем межосевое расстояние, а = 0, 55(d1 + d2) + h, (45) где h – высота ремня, мм (см. табл. 8), h=8 мм Подставив в формулу (45) численные значения указанных величин имеем: а = 0, 55(125 + 250) + 8 = 214, 25 мм Принимаем а = 214 мм 4. Определим длину ремня: L = 2а + (p (d1 + d2) / 2) + ((d2 - d1)2 / 4а). (46) Подставив в формулу (46) известные величины получим: L = 2а + (p (d1 + d2)/2) + ((d2 - d1)2/ 4а) = 2 × 214 +(3, 14(125 + 250)/2) + +((250– 125)2/4 × 214) = 996, 9 мм. Длину клинового ремня уточняем по стандартному ряду: 400, 450, 500, 560, 630, 710, 800, 900, 1000, 1120, 1250, 1400, 1600, 1800, 1950, 2000, 2240, 2500, 2800, 3120, 3150, 3200, 3255, 3285, 3325, 3550, 4000, 4500, 5000, 5600, 6300 мм. Принимаем L = 1000 мм 5. Уточняем межосевое расстояние передачи
Подставив в формулу (47) известные величины получим: а = = 195, 6 мм. Принимаем а = 196 мм 6. Определим угол обхвата ремнем ведущего шкива a1 = 180° - 57° (d2 - d1)/а ³ [a], (48) где a1 для нашего случая должно быть: a1 ³ 90°. По формуле (48) получаем:
7. Определим скорость ремня ν, м/с: ν = p d1 n1 / (60 × 103) £ [ν ], (49) где d1, n1 – соответственно диаметр ведущего шкива, мм и его частота вращения, об/мин. (см. раздел 1., п.3 для определения n1 и раздел 1, п.5 для определения d1); [ν ] = 25 м/с – для клиновых ремней. Получаем, что ν согласно формуле (49) равно: ν = p d1 n1 / (60 × 103)= 3, 14 × 125 × 953 / (60 × 103)= 6, 23 м/с. 8. Определим допускаемую мощность, передаваемую одним клиновым ремнем [Pn], кВт: [Pn] =[P0] Ср Сa СL Сz, (50) где [P0] – допускаемая приведенная мощность, передаваемая одним клиновым ремнем, выбирается по табл. 10, в зависимости от типа ремня, его сечения, скорости ν, м/с и диаметра ведущего шкива d1, мм; С – поправочные коэффициенты, выбираем по табл. 11. Получаем: [P0] = 2 кВт Ср = 0, 9, Сa = 0, 89, СL = 0, 89, Сz = 0, 95. Подставим известные величины в формулу (50) имеем: [Pn] =[P0] Ср Сa СL Сz = 2 9. Определим количество клиновых ремней:
где Рном – номинальная мощность двигателя, кВт, согласно расчетам (раздел 1., п.3 «Кинематический расчет привода») Рном = 3 кВт. Получаем, что Окончательно принимаем Z =2. 10. Определим силу предварительного натяжения F0, Н:
где значение Рном, СL, Z, Сa и Ср определялись ранее. Подставив в формулу (52) численные значения известных величин получим:
11. Определим окружную силу, передаваемую комплектом клиновых ремней: Ft = Рном × 103/ν, (53) Где Рном, кВт; ν, м/с определялись ранее. Получаем, что Ft = Рном × 103/ν = 3 × 103/6, 23 = 481 н. 12. Определим силы натяжения ведущей F1 и ведомой F2 ветви, Н: F1 = F0 + Ft / 2 Z. (54) F2 = F0 - Ft /2 Z. Согласно формулам (54) имеем, что: F1 = F0 + Ft / 2 Z =227, 4 + 481 / 2 F2 = F0 - Ft /2 Z = 227, 4 – 481 / 2 13. Определим силу давления на вал F0n, Н:
Подставив в выражение (55) известные величины получаем, что:
Чтобы проверить достоверность проведенных решений проверим прочность одного клинового ремня под максимальным напряжением в сечении ведущей ветви smax, МПа smax = s1 + su + sν £ [s]р, (56) где σ 1 – напряжение растяжения, МПа.
А – площадь поперечного сечения ремня, А = 81 (табл. 9)
su – напряжение изгиба, МПа, где где Еu = 80…100 н/мм2 – модуль продольной упругости при изгибе для прорезиненных ремней; h – высота сечения клинового ремня
sν = p ν 2 × 10-6 – напряжение от центробежных сил, МПа sν = p ν 2 × 10-6 = 1300 × 6, 232 × 10-6 = 0, 05 МПа p – плотность материала ремня, кг/м3, p = 1250…1400 кг/м3 [s]p- допускаемое напряжение растяжения, МПа [s]p = 10 МПа – для клиновых ремней. Подставим в формулу (56) известные величины, получим: smax = s1 + su + sν = 4, 28 + 5, 16+ 0, 05 = 9, 49 < 10 МПа.
|

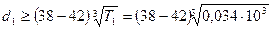 = 123, 1 … 136, 06 мм.
= 123, 1 … 136, 06 мм.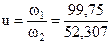 =
=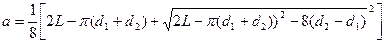 . (47)
. (47)
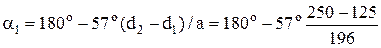 = 144°.
= 144°. 0, 9 × 0, 89 × 0, 89 × 0, 95 = 1, 35 кВт.
0, 9 × 0, 89 × 0, 89 × 0, 95 = 1, 35 кВт.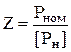 , (51)
, (51)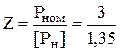 = 2, 2.
= 2, 2. , (52)
, (52)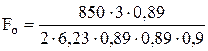 = 227, 4 Н.
= 227, 4 Н. . (55)
. (55) = 865, 08 Н.
= 865, 08 Н.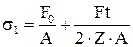 ,
, = 4, 28 МПа
= 4, 28 МПа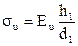 ,
,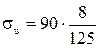 = 5, 16 МПа
= 5, 16 МПа


