Моделирование СИ методом аналогий
При моделировании средств измерения широкое распространение получил метод аналогий, который заключается в следующем. Для цепей различной физической природы устанавливается аналогия обобщенных параметров: сил, скоростей, координат, и т.д. Эти аналогии сводятся в таблицу. При этом аналогами называются цепи различной физической природы, описываемые одной и той же системой интегродиффиренциальных уравнений В связи с тем, что имеется параллельное и последовательное соединение элементов в электрических и механических цепях, могут иметь место, по крайней мере, четыре аналогии параметров этих цепей, называемые прямыми: 1. параллельно 2. последовательно А так же четыре аналогии, называемые обратными: 1. параллельно 2. последовательно
Рис. 8.4. Схема механической цепи с параллельным соединением звеньев
На рис. 8.4 приведена схема механической цепи с параллельным соединением элементов, состоящей из пружины (1) с коэффициентом жесткости k, вязкого демпфера (2) с параметром демпфирования Rm и приведенной массой m подвижных частей, к которым приложена активная сила F. Примером такой цепи может служить механическая измерительная цепь емкостного преобразователя (рис. 8.5а).
a) б)
Рис. 8.5. Емкостный преобразователь: а) конструкция; б) схема взаимодействия элементов
Емкостный измерительный преобразователь давления P состоит из конденсатора, образованного неподвижной обкладкой 2 и мембраной 1, подключенного через сопротивление R к источнику напряжения U. Схематическое изображение основных элементов емкостного преобразователя показан на рис. 8.5, б. Механическое перемещение мембраны соответствует перемещению массы m под действием силы F, которое ограничено упругой силой пружины (мембраны) К. Демпфирующее действие объемов воздуха между мембраной и неподвижной обкладкой учитывается коэффициентом демпфирования Rm. Согласно принципу Д’Аламдера
где Fm- сила инерции; F1 и F2 – силы, соответственно развиваемые пружиной и демпфером; X – перемещение (обобщенная координата) отсчитываемое от исходного состояния равновесия (F=0). Уравнение (8.4) можно записать в виде
где
На рис. 8.6 изображена последовательная электрическая цепь, состоящая из источника напряжения U, конденсатора С, катушки индуктивности L и активного сопротивления R.
Рис. 8.6. Последовательная электрическая цепь
Используя второй закон Кирхгофа можно записать уравнение для этой цепи в виде
Откуда с учетом того, что ток i в цепи и электрический заряд q, накопленный элементами этой цепи, связаны соотношением
Уравнение (8.6) можно записать в виде
Сравнивая уравнения (8.5) и (8.8) можно установить аналогии параметров: механическая цепь параллельная ó электрическая цепь последовательная. В таблице 8.1 приведены аналогии обобщенных параметров механических и электрических цепей. Метод аналогии позволяет проводить аналоговое моделирование механических цепей с помощью электрических цепей.
Таблица 8.1 Аналогии обобщенных параметров механической и электрической цепей
|

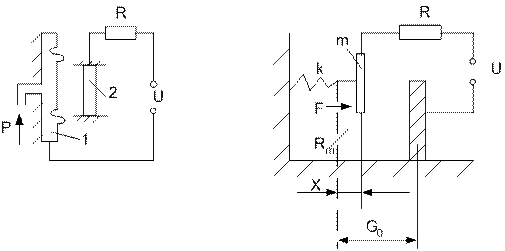
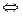 параллельно;
параллельно;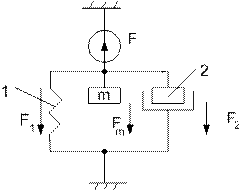
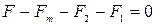 ,
,
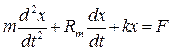 ,
,
 ,
, ,
,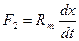 .
.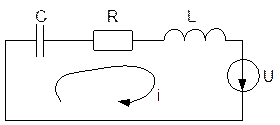
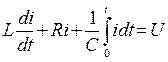 .
.
 .
.
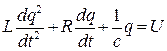 ,
,
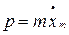 ,
,  Обобщённый импульс
Обобщённый импульс
 ,
, 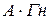 потокосцепление
потокосцепление
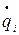
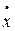 ,
, 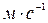 скорость
скорость
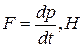 сила
сила
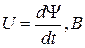 напряжение
напряжение
 ток
ток
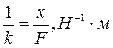 эластичность
эластичность
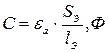 ёмкость
ёмкость
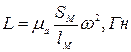 индуктивность
индуктивность
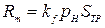 ,
,
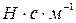 демпфирование, сопротивление потерь
демпфирование, сопротивление потерь
 механическая проводимость
механическая проводимость
 проводимость
проводимость
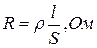 активное сопротивление
активное сопротивление
 жесткость упругих элементов
жесткость упругих элементов
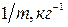 величина, обратная массе
величина, обратная массе



