Атомные функции распределения
Кристаллическую структуру легко описать аналитически, пользуясь общей формулой для узлов решетки. В отсутствие дальнего топологического или ориентационного порядка требуется новый язык. При этом попытка просто задать координаты всех N атомов Rl , R2,..., RN бесполезна, так как число N сколь угодно велико. С чем бы мы ни имели дело - с одной большой системой или с ансамблем похожих систем, - характеристики такого набора материала надо выражать через статистические функции вероятностей. Названные функции представляют собой не что иное, как одночастичную, двухчастичную, трехчастичную и т. д. плотности вероятности, n (1), n (1, 2), n (1, 2, 3).... Формально они определяются соотношением: dP (1, 2,..., s) = n (1, 2,..., s) d 1 d 2... ds, (3.8) Здесь dP есть вероятность найти атом в объеме d 1 вблизи точки 1, в объеме d 2 вблизи точки 2 и т. д. В большинстве задач достаточно считать, что рассматриваемые функции не зависят от времени, описывая лишь статическую конфигурацию атомов. При этом выборка производится так, что один и тот же атом можно считать дважды, только если вновь попасть в одну и ту же точку пространства. Из основного предположения о макроскопической однородности образца следует, что средняя плотность атомов в единице объема должна быть постоянной, т. е. n (1) = n = N / V независимо от положения точки 1. Интегрируя теперь выражение (3.8) по всем координатам, получаем
Видно, что вычисления упрощаются, если ввести каноническую функцию распределения g. Интеграл кратности s от функции g (1, 2,..., s) по единичному объему равен единице. Другими словами, величина g (1, 2,..., s) d 1...... ds даст нам вероятность найти именно такой тип расположения s-атомов из всех других возможных способов размещения их в пространстве при одной и той же средней плотности. Эти определения общепринятые; они приводятся лишь для того, чтобы стандартизовать наши обозначения. Почти все данные прямых измерений, относящиеся к расположению атомов в конденсированной среде, описываются бинарной функцией распределения g (1, 2). В силу пространственной однородности системы эта функция может зависеть только от вектора g (l, 2) = g ( Для идеального монокристалла эта функция g(
Отсутствие дальнего топологического порядка (как в кристалле с дислокациями) приведет в основном к уширению и размытости далеких пиков этой функции в однородный континуум. Масштаб локального порядка можно определить как расстояние, за пределами которого функция
Рис. 3.12. Бинарная функция распределения для модели решетки, в которой дислокации разрушают дальний порядок.
В поликристаллическом образце этот масштаб характеризует размер кристаллитов. Однако, вводя статистические функции распределения, необходимо учесть и ориентационный беспорядок, который делает такой образец макроскопически изотропным. Как бы ни был велик каждый кристаллит, гипотетически бесконечный образец или ансамбль будет содержать такие кристаллиты со всеми возможными ориентациями. Парную функцию распределения (3.11) надо, следовательно, усреднить по всем направлениям векторов решетки
Рис.3.13. Радиальная функция распределения. а – для идеального кристалла; б – для поликристалла (с уширением за счет теплового движения).
Здесь N (l) есть число векторов решетки с одной и той же длиной Таким образом, неупорядоченную систему нельзя адекватно описать аналитически, не поднимаясь вверх по иерархической лестнице функций распределения. Оценим трех- и четырехчастичные функции распределения для поликристаллического образца.
Рис. 3.14. В поликристалле тройную функцию распределения g (1, 2, 3) можно ввести только для треугольников, принадлежащих кристаллической решетке.
В соответствии с принципом однородности функция g (1, 2, 3) зависит только от относительных координат
Желая сделать это выражение симметричным относительно точек 1, 2, 3, мы должны ввести еще одну дельта-функцию для третьей стороны треугольника, вершины которого расположены в данных точках (рис.3.14).
Недостатком этого выражения является то, что эта функция не удовлетворяет суперпозиционному приближению:
3.7.2. Аморфный или поликристаллический? Задача состоит в том, чтобы выяснить, чем физически отличается та или иная модель от других, ей альтернативных. Самые точные данные получаются при исследовании дифракции нейтронов и рентгеновских лучей, однако эти данные никогда не удается интерпретировать однозначно. В тех случаях, когда в рассеяние вносят вклад несколько различных химических элементов (как, например, в кварцевых стеклах), «распутать» эти вклады оказывается необычайно трудно и получить вполне определенный ответ обычно не удается. Однако даже в лучшем случае моноатомного материала типа аморфного кремния или германия все, что нам удается измерить, это радиальная функция распределения g (R). Что можно извлечь из этой функции? Как видно из рис. 3.15, она имеет некоторые «черты», допускающие физическую интерпретацию. В частности, эта функция должна обратиться в нуль на расстоянии, равном диаметру атомного остова; затем она возрастает, достигая максимума (пика) на некотором характерном расстоянии
Рис.3.15. Характерный вид радиальной функции распределения Площадь под этим пиком
есть координационное число данной структуры, например, z = 4. Аналогично следующий пик обусловлен второй координационной сферой и т. д. Однако фактически координационное число точно не определено и число атомов внутри каждой сферы становится все более и более неопределенным по мере того, как пики уширяются, сливаются друг с другом, а затем вообще теряются на фоне континуума, где g (R) ® 1. Для многих теоретических задач удобнее измерять функцию g (R) по отношению к этому фону: полная корреляционная функция
характеризует степень локального отклонения от статической однородности вблизи любого данного атома. Размер области упорядочения L в этом случае определяется эмпирически как расстояние, на котором функция h (R) обращается в нуль: h (R)» 0 при R > L. Эти общие характерные черты радиальной функции распределения естественным образом возникают в модели случайной сетки в аморфных полупроводниках. Например, в тетраэдрической сетке первая и вторая координационные сферы почти идентичны соответствующим координационным сферам в идеальной решетке алмаза; однако вращение тетраэдров вокруг соединяющей их связи изменяет расстояния до третьих соседей. В этом состоит простое физическое объяснение того, почему в радиальной функции распределения при переходе от кристаллического кремния к аморфному исчезает третий пик радиальной функции распределения. Вместе с тем трудно доказать с полной убедительностью, что эти черты не согласуются с моделью горячего кристалла или возмущенного поликристаллического беспорядка. Пусть, например, в результате тепловых колебаний атомы идеального кристалла отклонились случайным образом от узлов идеальной решетки, может быть так, как показано на рис. 3.15.
|

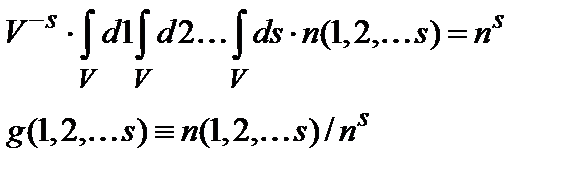 . (3.9)
. (3.9)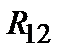 , соединяющего точки 1 и 2, т. е.
, соединяющего точки 1 и 2, т. е. (3.11)
(3.11) становится близкой к единице.
становится близкой к единице.
 . Иными словами, в конце концов, мы приходим к набору концентрических сферических оболочек, радиусы которых равны длинам всех возможных векторов решетки:
. Иными словами, в конце концов, мы приходим к набору концентрических сферических оболочек, радиусы которых равны длинам всех возможных векторов решетки: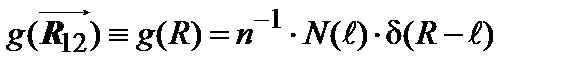 (3.12)
(3.12)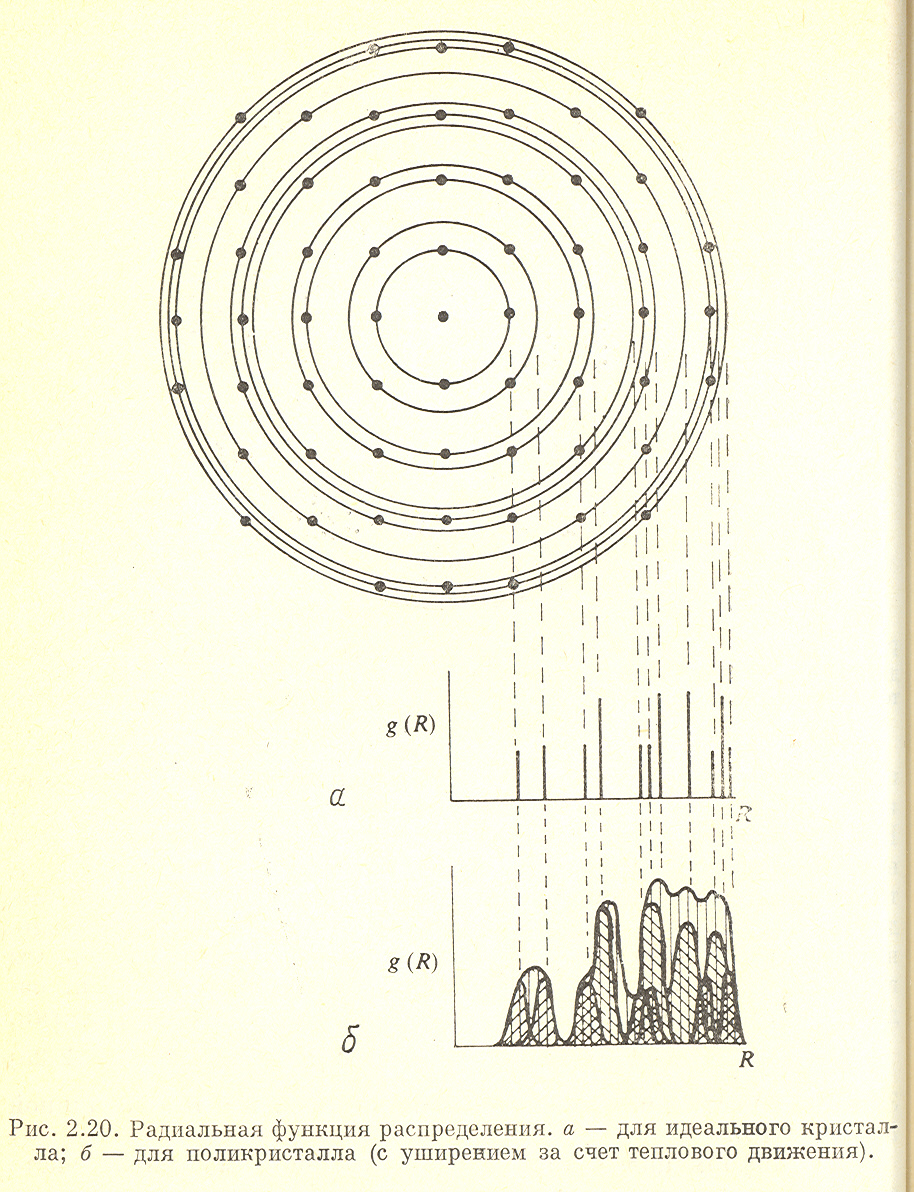
 . Вся информация о структуре изотропного материала часто содержится только в виде радиальной функции распределения g (R). В случае идеального поликристалла, содержащего лишь простые комбинации одной - двух химических компонент, бывает возможно восстановить структуру трехмерной локальной решетки по наблюдаемым на опыте пикам функции (3.12) (рис.3.13). Однако если эти пики сильно размыты из-за локального беспорядка тепловых колебаний или из-за недостаточного разрешения аппаратуры, то возникают неопределенности, и однозначное решение найти, как правило, не удается. В этом и состоит фундаментальная трудность физики топологически неупорядоченных материалов: картины локального расположения атомов в пространстве невозможно построить чисто аналитическим путем с помощью только ряда формальных операций над радиальной функцией распределения. Эти картины можно только угадать и убедиться, что догадка согласуется с данным видом функции распределения.
. Вся информация о структуре изотропного материала часто содержится только в виде радиальной функции распределения g (R). В случае идеального поликристалла, содержащего лишь простые комбинации одной - двух химических компонент, бывает возможно восстановить структуру трехмерной локальной решетки по наблюдаемым на опыте пикам функции (3.12) (рис.3.13). Однако если эти пики сильно размыты из-за локального беспорядка тепловых колебаний или из-за недостаточного разрешения аппаратуры, то возникают неопределенности, и однозначное решение найти, как правило, не удается. В этом и состоит фундаментальная трудность физики топологически неупорядоченных материалов: картины локального расположения атомов в пространстве невозможно построить чисто аналитическим путем с помощью только ряда формальных операций над радиальной функцией распределения. Эти картины можно только угадать и убедиться, что догадка согласуется с данным видом функции распределения.
 ,
, 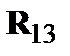 . В монокристалле эти векторы должны совпадать с векторами решетки, т. е.
. В монокристалле эти векторы должны совпадать с векторами решетки, т. е. . (3.13)
. (3.13) .(3.14)
.(3.14) (3.15)
(3.15) . Последнее обычно отождествляют с радиусом первой координационной сферы атомов (рис.3.15).
. Последнее обычно отождествляют с радиусом первой координационной сферы атомов (рис.3.15).

 (3.16)
(3.16)


