Случайное поле  можно определить, только задавая его статистические характеристики. Введем различные функции распределения для величин
можно определить, только задавая его статистические характеристики. Введем различные функции распределения для величин  . Так, функция
. Так, функция 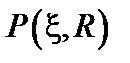 определяет плотность вероятности найти случайную величину
определяет плотность вероятности найти случайную величину  в интервале
в интервале 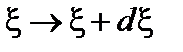 точке R. В силу предполагаемой однородности рассматриваемого поля эта функция не должна зависеть от R.
точке R. В силу предполагаемой однородности рассматриваемого поля эта функция не должна зависеть от R.
Предположим для простоты, что любая постоянная компонента поля, например среднее значение потенциала, исключена из рассмотрения, т. е. среднее значение  равно нулю. Это среднее значение можно представить:
равно нулю. Это среднее значение можно представить:
1. в виде интеграла по большому, но конечному объему V, в котором определен вектор R;
2. в виде интеграла по статистическому ансамблю очень большого числа одинаковых объемов; в таком ансамбле величина  в любой точке пространства принимает все возможные свои значения.
в любой точке пространства принимает все возможные свои значения.
Утверждение о равенстве двух указанных интегралов основывается на существовании эргодической гипотезы:
 . (4.1)
. (4.1)
На первый взгляд, функцией  может быть любая положительная функция, удовлетворяющая условию нормировки (интеграл от нее по всему объему должен быть равен единице).
может быть любая положительная функция, удовлетворяющая условию нормировки (интеграл от нее по всему объему должен быть равен единице).
Однако этого еще недостаточно для адекватной характеристики случайного поля. Говоря математическим языком, статистические характеристики случайного поля можно полностью определить, только задавая функционал  , представляющий собой предельный случай s -точечной функции распределения при
, представляющий собой предельный случай s -точечной функции распределения при  .
.
Надо ввести двухточечные, трехточечные и т. д. функции распределения: в общем случае s-точечная функция распределения  определяет вероятность того, что
определяет вероятность того, что  принимает значение
принимает значение  в точке
в точке 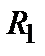 ,
,  - в точке
- в точке  и т. д. Только в нефизическом случае патологически разрывного поля можно предположить, что величины
и т. д. Только в нефизическом случае патологически разрывного поля можно предположить, что величины  в «соседних» точках распределены независимо.
в «соседних» точках распределены независимо.
Функции распределения должны удовлетворять ряду тождеств:
Так, интегрируя величину 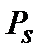 по любой пространственной переменной (например,
по любой пространственной переменной (например, 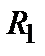 ) или усредняя ее по всему ансамблю полевой переменной
) или усредняя ее по всему ансамблю полевой переменной  мы должны получить функцию
мы должны получить функцию 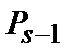 .
.
Далее, значения случайного поля  и
и  в двух точках
в двух точках 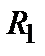 и
и  при
при  должны быть статистически независимы.
должны быть статистически независимы.
Если поле не только однородно, но и изотропно, то двухточечная функция распределения заметно упрощается: она непременно должна иметь вид:  .
.
Неявно принятое предположение о кусочной непрерывности функции  приводит к тому, что величины
приводит к тому, что величины  и
и  стремятся к одному и тому же значению, когда
стремятся к одному и тому же значению, когда 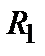 стремится к
стремится к  . Таким образом, имеем:
. Таким образом, имеем:
 (4.2)
(4.2)
С учетом этих ограничений функция  , описывая распределение двух величин
, описывая распределение двух величин  и
и  , зависит от трех переменных и ее трудно выразить в простом виде. Здесь опять теория беспорядка замещения в решетке указывает нам подходящий способ описания основных характеристик функции
, зависит от трех переменных и ее трудно выразить в простом виде. Здесь опять теория беспорядка замещения в решетке указывает нам подходящий способ описания основных характеристик функции  . Введем автокорреляционную функцию поля следующим образом:
. Введем автокорреляционную функцию поля следующим образом:
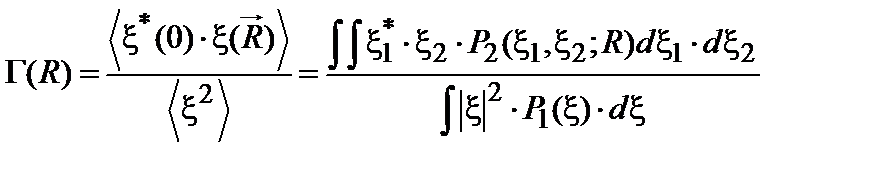 . (4.3)
. (4.3)
В выражениях такого типа удобно рассматривать x как комплексную переменную, вещественность которой в дальнейшем легко будет обеспечить с помощью тривиальных дополнительных условий. Как видно, функция  будет монотонно уменьшаться при увеличении R, изменяясь в следующих пределах:
будет монотонно уменьшаться при увеличении R, изменяясь в следующих пределах:
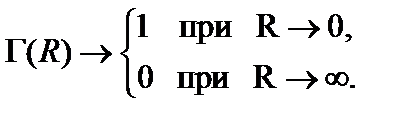 (4.4)
(4.4)
Здесь ясно видна аналогия с параметром порядка и с полной корреляционной функцией. Длина L будет определять типичный пространственный размер любой топологической черты поля  , будь то «пик» или «долина».
, будь то «пик» или «долина».
Однородность поля  можно интерпретировать как трансляционную инвариантность в статистическом смысле. Для описания такого поля естественно воспользоваться плоскими волнами
можно интерпретировать как трансляционную инвариантность в статистическом смысле. Для описания такого поля естественно воспользоваться плоскими волнами  , для которых волновые векторы q выбираются так, чтобы удовлетворить соответствующим граничным условиям в большом объеме V. Для любого компонента данного ансамбля случайных полей (любой реализации) можно ввести представление Фурье:
, для которых волновые векторы q выбираются так, чтобы удовлетворить соответствующим граничным условиям в большом объеме V. Для любого компонента данного ансамбля случайных полей (любой реализации) можно ввести представление Фурье:
 .
.
Комплексная амплитуда  явно определяется обратным интегральным преобразованием:
явно определяется обратным интегральным преобразованием:  .
.
Вычислим теперь автокорреляционную функцию. Пользуясь эргодической гипотезой, мы можем выполнить следующие стандартные преобразования:
 (4.5)
(4.5)
Этот результат совершенно аналогичен ранее полученному и справедлив для любого члена ансамбля. Определим спектральную плотность поля (или спектр мощности) равенством:
 . (4.6)
. (4.6)
Основную роль для дальнейшего играет теорема Винера - Хинчина: для любого случайного поля спектральная плотность есть фуръе-образ автокорреляционной функции.
Зная общие свойства функции  , мы можем сделать определенные выводы и о соответствующих свойствах
, мы можем сделать определенные выводы и о соответствующих свойствах  . Последняя функция должна быть положительно определенной; для изотропного поля она может зависеть только от волнового числа q, а не от направления в обратном пространстве. Исходя из условий (4.6) и пользуясь стандартными приемами исследования интегралов Фурье, можно показать, что
. Последняя функция должна быть положительно определенной; для изотропного поля она может зависеть только от волнового числа q, а не от направления в обратном пространстве. Исходя из условий (4.6) и пользуясь стандартными приемами исследования интегралов Фурье, можно показать, что  стремится к нулю, когда число
стремится к нулю, когда число  становится больше обратной длины корреляции
становится больше обратной длины корреляции  (рис. 4.1) Очевидно, спектральная плотность составляет необходимый элемент описания любого случайного поля. В какой мере она достаточна для этой цели? Перепишем равенство (4.6) в виде:
(рис. 4.1) Очевидно, спектральная плотность составляет необходимый элемент описания любого случайного поля. В какой мере она достаточна для этой цели? Перепишем равенство (4.6) в виде:
 . (4.7)
. (4.7)

а б
Рис. 4.1. а - автокорреляционная функция; 6 - спектральная плотность.
Видно теперь, что это равенство определяет амплитуду каждой (комплексной) Фурье-компоненты поля. Если бы мы знали еще и все фазы 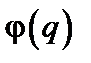 , то знали бы поле
, то знали бы поле  однозначно. Можно думать, что случайный характер поля проявляется как раз в статистических свойствах фаз различных компонент Фурье, фигурирующих в формуле (4.7).
однозначно. Можно думать, что случайный характер поля проявляется как раз в статистических свойствах фаз различных компонент Фурье, фигурирующих в формуле (4.7).

 можно определить, только задавая его статистические характеристики. Введем различные функции распределения для величин
можно определить, только задавая его статистические характеристики. Введем различные функции распределения для величин 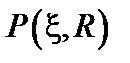 определяет плотность вероятности найти случайную величину
определяет плотность вероятности найти случайную величину  в интервале
в интервале 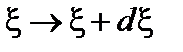 точке R. В силу предполагаемой однородности рассматриваемого поля эта функция не должна зависеть от R.
точке R. В силу предполагаемой однородности рассматриваемого поля эта функция не должна зависеть от R. . (4.1)
. (4.1) может быть любая положительная функция, удовлетворяющая условию нормировки (интеграл от нее по всему объему должен быть равен единице).
может быть любая положительная функция, удовлетворяющая условию нормировки (интеграл от нее по всему объему должен быть равен единице). , представляющий собой предельный случай s -точечной функции распределения при
, представляющий собой предельный случай s -точечной функции распределения при  .
. определяет вероятность того, что
определяет вероятность того, что  в точке
в точке 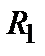 ,
,  - в точке
- в точке  и т. д. Только в нефизическом случае патологически разрывного поля можно предположить, что величины
и т. д. Только в нефизическом случае патологически разрывного поля можно предположить, что величины 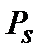 по любой пространственной переменной (например,
по любой пространственной переменной (например, 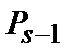 .
. должны быть статистически независимы.
должны быть статистически независимы. .
. приводит к тому, что величины
приводит к тому, что величины  (4.2)
(4.2) , описывая распределение двух величин
, описывая распределение двух величин 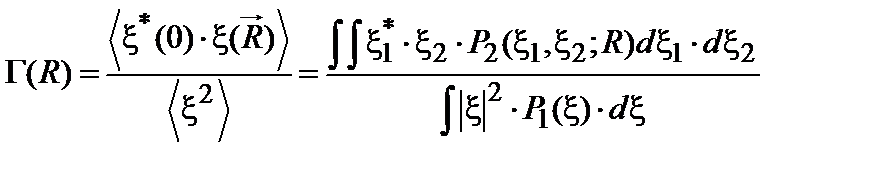 . (4.3)
. (4.3) будет монотонно уменьшаться при увеличении R, изменяясь в следующих пределах:
будет монотонно уменьшаться при увеличении R, изменяясь в следующих пределах: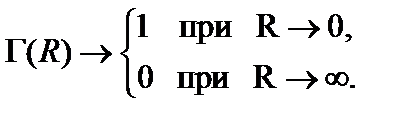 (4.4)
(4.4) , для которых волновые векторы q выбираются так, чтобы удовлетворить соответствующим граничным условиям в большом объеме V. Для любого компонента данного ансамбля случайных полей (любой реализации) можно ввести представление Фурье:
, для которых волновые векторы q выбираются так, чтобы удовлетворить соответствующим граничным условиям в большом объеме V. Для любого компонента данного ансамбля случайных полей (любой реализации) можно ввести представление Фурье: .
. явно определяется обратным интегральным преобразованием:
явно определяется обратным интегральным преобразованием:  .
. (4.5)
(4.5) . (4.6)
. (4.6) . Последняя функция должна быть положительно определенной; для изотропного поля она может зависеть только от волнового числа q, а не от направления в обратном пространстве. Исходя из условий (4.6) и пользуясь стандартными приемами исследования интегралов Фурье, можно показать, что
. Последняя функция должна быть положительно определенной; для изотропного поля она может зависеть только от волнового числа q, а не от направления в обратном пространстве. Исходя из условий (4.6) и пользуясь стандартными приемами исследования интегралов Фурье, можно показать, что  становится больше обратной длины корреляции
становится больше обратной длины корреляции  (рис. 4.1) Очевидно, спектральная плотность составляет необходимый элемент описания любого случайного поля. В какой мере она достаточна для этой цели? Перепишем равенство (4.6) в виде:
(рис. 4.1) Очевидно, спектральная плотность составляет необходимый элемент описания любого случайного поля. В какой мере она достаточна для этой цели? Перепишем равенство (4.6) в виде: . (4.7)
. (4.7)
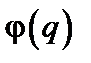 , то знали бы поле
, то знали бы поле 


