Возбуждения в одномерных системах
Рассмотрим возбуждения в неупорядоченной одномерной цепочке. 1. Диагональный беспорядок уровней энергии - во-первых, могут иметь место физические или химические различия между компонентами периодически расположенных ячеек периодической цепочки; - во-вторых, возможны флуктуации относительных расстояний 2. Наиболее серьезное ограничение полезности одномерных моделей с теоретической точки зрения связано с обязательной топологической их упорядоченностью. Это означает, например, что «индекс узла» j в уравнениях (6.10) всегда эквивалентен «вектору» периодической решетки, в которой среднее межатомное расстояние такое же, как и в настоящей системе. Говоря математическим языком, нет возможности отличить беспорядок замещения в «одномерном сплаве» от эффектов, связанных со случайным характером расстояний между атомами в «одномерном стекле» или «одномерной жидкости». Физические допущения, лежащие в основе модели, влияют лишь на статистические характеристики величин, фигурирующих в качестве диагональных и недиагональных элементов в уравнениях (6.10). 3. Неизбежность последовательности атомов (в случае одномерной модели) позволяет сформулировать другой поход к поиску метода решения уравнений (10). Мы не сильно потеряем в общности, если допустим, что величины
Введем матрицу переноса, которая генерирует последовательные дифференциальные уравнения вида (6.10).
Здесь Отсюда следует, что возбуждение Таким образом, матрица переноса однозначно связана с каждой ячейкой решетки. Распространение возбуждения вдоль цепочки можно изобразить в виде матричного произведения последовательности соответствующих матриц. Пользуясь соотношением (16), получаем:
Для упорядоченной системы, в которой все матрицы переноса одинаковы, можно записать
Влияние беспорядка сводится к тому, что матрицы переноса меняются от ячейки к ячейке за счет случайных вариаций элементов матрицы (6.16). Другими словами, матрица переноса Рассмотрим более конкретную задачу о движении электрона в поле одномерного случайного потенциала, имея в виду беспорядок замещения, мы можем построить модель сплава Кронига - Пенни (рис. 6.1 а). Узлам решетки в этой модели приписываются дельтообразные потенциалы с различными «силами» Можно ввести и модель жидкости Кронига - Пенни (рис. 6.1 б), в которой случайной переменной служит расстояние между соседними дельта-функциями В обоих случаях обычная теория модели Кронига - Пенни для периодической цепочки подсказывает нам, что решение уравнения Шредингера при энергии Пусть координата
Рис.6.1. Модели Кронига - Пенни: а - «сплав»; б - «жидкость».
Коэффициенты здесь пока произвольны. Однако функцию (6.19) по прохождении через сингулярность
Подставляя выражение (6.19) в условия (6.20), получаем линейные уравнения для последовательных амплитуд возбуждения
В матричной форме эти уравнения имеют вид:
Если отвлечься от физического смысла возбуждения 5. Все же то, что мы сейчас рассмотрели, есть достаточно частный случай. Любую одномерную потенциальную энергию
Рис.6.2. а - непрерывная случайная потенциальная энергия
Заметим, что в двух- и трех- мерном случаях все рассмотренные выше обобщения оказываются несправедливыми из-за возможности обхода некоторого узла.
|

 и недиагональный беспорядок матричных элементов
и недиагональный беспорядок матричных элементов  потенциальной энергии могут быть связаны с двумя причинами:
потенциальной энергии могут быть связаны с двумя причинами: между атомными центрами в цепочке, а беспорядок получается как следствие этих флуктуации.
между атомными центрами в цепочке, а беспорядок получается как следствие этих флуктуации. . (6.15)
. (6.15) или
или  (6.16)
(6.16) - вектор амплитуд двух соседних ячеек
- вектор амплитуд двух соседних ячеек  , а вектор
, а вектор 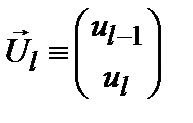 - амплитуды в предыдущей паре узлов.
- амплитуды в предыдущей паре узлов. в
в  - м узле порождается соответствующим возбуждением в предыдущем узле, умноженным на матрицу переноса
- м узле порождается соответствующим возбуждением в предыдущем узле, умноженным на матрицу переноса  . В простейшем случае
. В простейшем случае 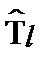 - это матрица 2 × 2, компоненты которой даются выражением (6.16).
- это матрица 2 × 2, компоненты которой даются выражением (6.16). . (6.17)
. (6.17) . (6.18)
. (6.18) есть случайная функция номера узла
есть случайная функция номера узла  ; функция распределения ее значений определяется физическими особенностями данной модели.
; функция распределения ее значений определяется физическими особенностями данной модели.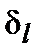 .
. .
. строится из волновых функций свободного электрона с волновыми числами
строится из волновых функций свободного электрона с волновыми числами  .
. принадлежит l -му «открытому промежутку» (
принадлежит l -му «открытому промежутку» (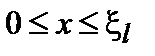 ). Тогда указанную функцию можно записать в виде:
). Тогда указанную функцию можно записать в виде: . (6.19)
. (6.19)
 из соседнего промежутка. Условия сшивания при таком переходе имеют вид:
из соседнего промежутка. Условия сшивания при таком переходе имеют вид: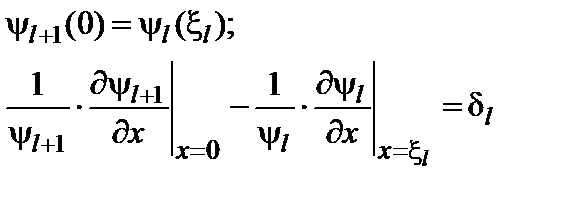 . (6.20)
. (6.20) .
. (6.21)
(6.21) , то полученное выражение имеет такую же форму, что и соотношение (16). Для упорядоченной системы все матрицы переноса
, то полученное выражение имеет такую же форму, что и соотношение (16). Для упорядоченной системы все матрицы переноса  были бы, как и в формуле (6.18), одинаковы для всех узлов. Для наших неупорядоченных моделей элементы матриц
были бы, как и в формуле (6.18), одинаковы для всех узлов. Для наших неупорядоченных моделей элементы матриц  можно представить в виде одномерной последовательности «атомных потенциалов»
можно представить в виде одномерной последовательности «атомных потенциалов»  , разделенных участками (может быть, бесконечно узкими), на которых потенциальная энергия равна нулю (рис. 6.1). Таким образом, математическая задача сводится к исследованию возбуждений, распространение которых вдоль цепочки описывается уравнениями типа (6.16); при этом элементы матрицы
, разделенных участками (может быть, бесконечно узкими), на которых потенциальная энергия равна нулю (рис. 6.1). Таким образом, математическая задача сводится к исследованию возбуждений, распространение которых вдоль цепочки описывается уравнениями типа (6.16); при этом элементы матрицы  суть случайные переменные. Метод матрицы переноса (6.16) можно использовать для любых теоретических моделей возбуждений в одномерной цепочке. Случай, когда возбуждение
суть случайные переменные. Метод матрицы переноса (6.16) можно использовать для любых теоретических моделей возбуждений в одномерной цепочке. Случай, когда возбуждение 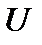 имеет только две компоненты, обладает достаточной общностью. Он описывает большинство моделей колебательных или электронных возбуждений в цепочке «сплава» или «жидкости». Эти физические задачи математически сводятся к изучению результатов преобразования двумерного вектора
имеет только две компоненты, обладает достаточной общностью. Он описывает большинство моделей колебательных или электронных возбуждений в цепочке «сплава» или «жидкости». Эти физические задачи математически сводятся к изучению результатов преобразования двумерного вектора 
 ; б - ее разбиение в нулевых точках (со случайными расстояниями x между ними) на одномерную цепочку случайных ячеистых «потенциалов»
; б - ее разбиение в нулевых точках (со случайными расстояниями x между ними) на одномерную цепочку случайных ячеистых «потенциалов»  .
.


