Неупорядоченная цепочкаматематически характеризуется случайной последовательностью неодинаковых матриц переноса  , произведение которых (6.17) описывает распространение возбуждениявдоль цепочки. Для каждой такой цепочки при помощи численных расчетов можнонайти стационарные состояния, удовлетворяющие граничным условиям вида (6.23). Однако главная задача состоит в отыскании спектрального распределения для ансамбля цепочек, в котором различные типы матриц переноса распределены случайно с какими-то заранее заданными вероятностями.
, произведение которых (6.17) описывает распространение возбуждениявдоль цепочки. Для каждой такой цепочки при помощи численных расчетов можнонайти стационарные состояния, удовлетворяющие граничным условиям вида (6.23). Однако главная задача состоит в отыскании спектрального распределения для ансамбля цепочек, в котором различные типы матриц переноса распределены случайно с какими-то заранее заданными вероятностями.
1. Наиболее прост пример случайного бинарного сплава, в котором матрицы переноса  и
и  распределены вдоль цепочки случайным образом с относительными концентрациями
распределены вдоль цепочки случайным образом с относительными концентрациями  и
и  .
.
2. Все типы одномерного «пространственного» беспорядка -«одномерное стекло», «одномерную жидкость» и т. д.- можно описать единым образом, последовательно выбирая матрицы переноса из множества  , в котором задана функция распределения
, в котором задана функция распределения  межатомных расстояний x. Например, теория электронных состояний в «одномерном жидкомметалле» основывается на изучении цепочки, матрицы переноса для которой даются выражениями аналогичными (6.21). При этом элементы матриц зависят от выбора чисел
межатомных расстояний x. Например, теория электронных состояний в «одномерном жидкомметалле» основывается на изучении цепочки, матрицы переноса для которой даются выражениями аналогичными (6.21). При этом элементы матриц зависят от выбора чисел  на каждом шаге.
на каждом шаге.
Как отмечалось, в спектре периодической цепочки имеется запрещенная зона, если собственные значения матрицы переноса вещественны. Пусть условие возникновения запрещенной зоны (25) выполняется, когда спектральная переменная c принадлежит области  . Для различных значений параметра
. Для различных значений параметра  , (или, может быть, для разных типов атомов) указанные области будут разными.
, (или, может быть, для разных типов атомов) указанные области будут разными.
Допустим далее, что все эти области в какой-то мере перекрываются: существует область  , общая для всех
, общая для всех  при любых физически возможных значениях x (или для всех сортов атомов в сплаве). Тогда на каждом шаге вдоль любой неупорядоченной цепочки, построенной из матриц
при любых физически возможных значениях x (или для всех сортов атомов в сплаве). Тогда на каждом шаге вдоль любой неупорядоченной цепочки, построенной из матриц  , возбуждение, которому отвечает спектральная переменная l, лежащая в области
, возбуждение, которому отвечает спектральная переменная l, лежащая в области 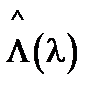 , будет наталкиваться на матрицы перехода с вещественными собственными значениями.При этом вектор возбуждения «застревает». Таким образом, область
, будет наталкиваться на матрицы перехода с вещественными собственными значениями.При этом вектор возбуждения «застревает». Таким образом, область  оказывается запрещенной зоной в спектре любой цепочки.
оказывается запрещенной зоной в спектре любой цепочки.
В общем случае может быть доказана теорема: любой области спектра, которой отвечают запрещенные зоны в спектрах как беспримесной цепочки типа А, так и беспримесной цепочки типа В, соответствует и запрещенная зона в спектре решетки, построенной из произвольной смеси атомов А и В.
Например, частоты колебаний изотопически неупорядоченного сплава, представляющего собой смесь легких (0) и тяжелых атомов (1) с массами соответственно  и
и  . Например, для беспримесных цепочек из атомов типа (0), фононный спектр имеет вид:
. Например, для беспримесных цепочек из атомов типа (0), фононный спектр имеет вид:
 . (6.27)
. (6.27)
Здесь константа Ф выражается через силовые постоянные, а величине  можно сопоставить волновой вектор возбуждения q. Максимальная частота
можно сопоставить волновой вектор возбуждения q. Максимальная частота  в этой зоне равна
в этой зоне равна  , она лежит выше соответствующего предельного значения для беспримесной цепочки атомов с массами
, она лежит выше соответствующего предельного значения для беспримесной цепочки атомов с массами  . Тогда из доказанной выше теоремы следует только, что в смешанной цепочке запрещены частоты колебаний, превышающие оба эти предельные значения. Иначе говоря, не существует нормальных колебаний с частотой, превышающей максимальную частоту колебаний периодической цепочки, составленной из самых легких атомов смеси.
. Тогда из доказанной выше теоремы следует только, что в смешанной цепочке запрещены частоты колебаний, превышающие оба эти предельные значения. Иначе говоря, не существует нормальных колебаний с частотой, превышающей максимальную частоту колебаний периодической цепочки, составленной из самых легких атомов смеси.
Эта общая теорема применима и к жидкости Кронига - Пенни, в которой одинаковые дельтообразные пики потенциальной энергии 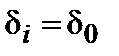 отстоят друг от друга на разных расстояниях
отстоят друг от друга на разных расстояниях  .
.
Оказывается, однако, что если отношение масс достаточно велико, то для некоторых волновых чисел возникают дополнительные узкие запрещенные зоны в спектре фононов. Допустим, прежде всего, что концентрация тяжелых атомов столь высока, что априорная вероятность встретить длинную непрерывную последовательность легких атомов очень мала. Говоря точнее, исключим произвольно из статистического ансамбля все цепочки, в которых подряд расположены более ( ) атома массы
) атома массы  . Тогда, любую неупорядоченную цепочку можно рассматривать как случайную совокупность элементов, выбранных из множества отрезков
. Тогда, любую неупорядоченную цепочку можно рассматривать как случайную совокупность элементов, выбранных из множества отрезков  переменной длины, каждый из которых содержит один атом массы
переменной длины, каждый из которых содержит один атом массы  и (s - 1) = 0, 1, 2,..., (р- 1) атомов массы
и (s - 1) = 0, 1, 2,..., (р- 1) атомов массы  . Пусть
. Пусть  – матрица переноса для такого отрезка, тогда в периодической цепочке из таких отрезков возникнет запрещенная зона
– матрица переноса для такого отрезка, тогда в периодической цепочке из таких отрезков возникнет запрещенная зона  . Теорема утверждает, что в неупорядоченной цепочке также возникнет запрещенная зона в области
. Теорема утверждает, что в неупорядоченной цепочке также возникнет запрещенная зона в области  , которая является общей для всех областей
, которая является общей для всех областей  при
при  . Следовательно, запрещенная зона в спектре рассмотренного ограниченного ансамбля неупорядоченных цепочек может иметь вид как на рис.6.3.
. Следовательно, запрещенная зона в спектре рассмотренного ограниченного ансамбля неупорядоченных цепочек может иметь вид как на рис.6.3.

Рис. 6.3. Общие запрещенные зоны для сплавов, не содержащих более четырех легких атомов. Отношение масс –  .
.
Для совершенно неупорядоченной цепочки, в которой нельзя полностью исключить вероятность обнаружения бесконечной последовательности атомов только с массой  , каждая из этих запрещенных зон должна быть в принципе бесконечно узкой. Однако более детальный анализ показывает, что выше каждой исключенной особой частоты лежит некоторая область настоящих уровней, соответствующих связанным примесным модам. Эти моды порож-даются «островками» легких атомов, отделенных друг от друга «морем» тяжелых атомов. Островок из р легких атомов обладает р различными модами. Каждая из них уширяется в узкую зону за счет взаимодействия (через тяжелые атомы) с другими подобными островками в цепочке. Результирующий колебательный спектр системы представляет собой просто сумму всех таких вкладов. Однако, так как вероятность обнаружить цепочку с очень длинной непрерывной последовательностью легких атомов очень мала, то наблюдению доступно лишь несколько мод, лежащих непосредственно под особой частотой. Таким образом, плотность состояний в этой точке меняется почти скачком (рис. 6.4).
, каждая из этих запрещенных зон должна быть в принципе бесконечно узкой. Однако более детальный анализ показывает, что выше каждой исключенной особой частоты лежит некоторая область настоящих уровней, соответствующих связанным примесным модам. Эти моды порож-даются «островками» легких атомов, отделенных друг от друга «морем» тяжелых атомов. Островок из р легких атомов обладает р различными модами. Каждая из них уширяется в узкую зону за счет взаимодействия (через тяжелые атомы) с другими подобными островками в цепочке. Результирующий колебательный спектр системы представляет собой просто сумму всех таких вкладов. Однако, так как вероятность обнаружить цепочку с очень длинной непрерывной последовательностью легких атомов очень мала, то наблюдению доступно лишь несколько мод, лежащих непосредственно под особой частотой. Таким образом, плотность состояний в этой точке меняется почти скачком (рис. 6.4).
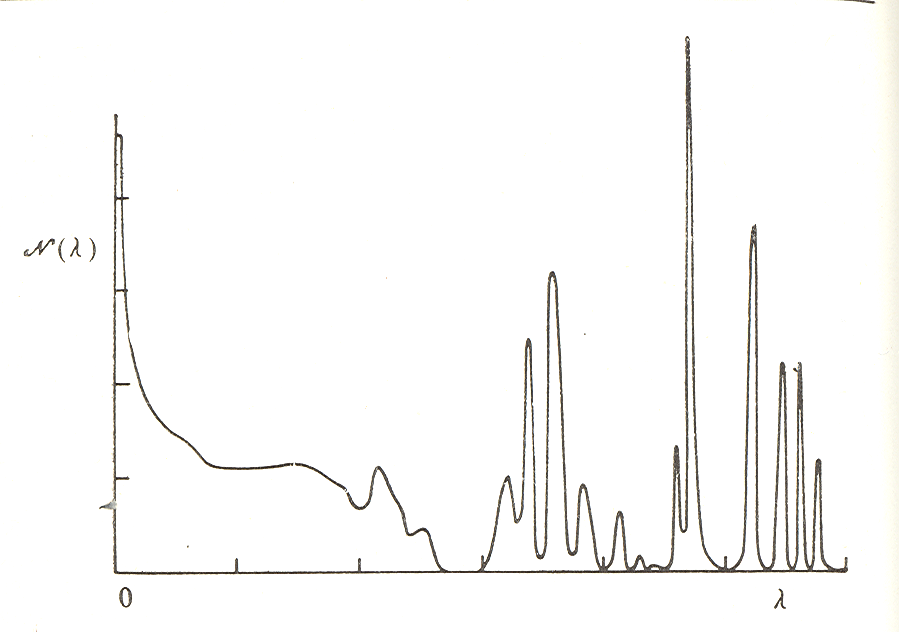
Рис. 6.4. Спектр неупорядоченной цепочки при отношении масс атомов в сплаве равном трем.
Физическая интерпретация этого явления в рамках представления об «островках» примеси наводит на мысль, что похожие эффекты можно наблюдать и в энергетическом спектре электронов в неупорядоченных одномерных сплавах, компоненты которых резко различны. Например, в модели Кронига - Пенни это означает, что «силы» дельта-функций  должны быть достаточно большими и достаточно сильно отличающимися друг от друга.
должны быть достаточно большими и достаточно сильно отличающимися друг от друга.

 , произведение которых (6.17) описывает распространение возбуждениявдоль цепочки. Для каждой такой цепочки при помощи численных расчетов можнонайти стационарные состояния, удовлетворяющие граничным условиям вида (6.23). Однако главная задача состоит в отыскании спектрального распределения для ансамбля цепочек, в котором различные типы матриц переноса распределены случайно с какими-то заранее заданными вероятностями.
, произведение которых (6.17) описывает распространение возбуждениявдоль цепочки. Для каждой такой цепочки при помощи численных расчетов можнонайти стационарные состояния, удовлетворяющие граничным условиям вида (6.23). Однако главная задача состоит в отыскании спектрального распределения для ансамбля цепочек, в котором различные типы матриц переноса распределены случайно с какими-то заранее заданными вероятностями. и
и  распределены вдоль цепочки случайным образом с относительными концентрациями
распределены вдоль цепочки случайным образом с относительными концентрациями  и
и  .
. , в котором задана функция распределения
, в котором задана функция распределения  межатомных расстояний x. Например, теория электронных состояний в «одномерном жидкомметалле» основывается на изучении цепочки, матрицы переноса для которой даются выражениями аналогичными (6.21). При этом элементы матриц зависят от выбора чисел
межатомных расстояний x. Например, теория электронных состояний в «одномерном жидкомметалле» основывается на изучении цепочки, матрицы переноса для которой даются выражениями аналогичными (6.21). При этом элементы матриц зависят от выбора чисел  на каждом шаге.
на каждом шаге. . Для различных значений параметра
. Для различных значений параметра  , (или, может быть, для разных типов атомов) указанные области будут разными.
, (или, может быть, для разных типов атомов) указанные области будут разными. , общая для всех
, общая для всех  при любых физически возможных значениях x (или для всех сортов атомов в сплаве). Тогда на каждом шаге вдоль любой неупорядоченной цепочки, построенной из матриц
при любых физически возможных значениях x (или для всех сортов атомов в сплаве). Тогда на каждом шаге вдоль любой неупорядоченной цепочки, построенной из матриц 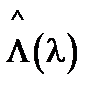 , будет наталкиваться на матрицы перехода с вещественными собственными значениями.При этом вектор возбуждения «застревает». Таким образом, область
, будет наталкиваться на матрицы перехода с вещественными собственными значениями.При этом вектор возбуждения «застревает». Таким образом, область  оказывается запрещенной зоной в спектре любой цепочки.
оказывается запрещенной зоной в спектре любой цепочки. и
и  . Например, для беспримесных цепочек из атомов типа (0), фононный спектр имеет вид:
. Например, для беспримесных цепочек из атомов типа (0), фононный спектр имеет вид: . (6.27)
. (6.27) можно сопоставить волновой вектор возбуждения q. Максимальная частота
можно сопоставить волновой вектор возбуждения q. Максимальная частота  в этой зоне равна
в этой зоне равна  , она лежит выше соответствующего предельного значения для беспримесной цепочки атомов с массами
, она лежит выше соответствующего предельного значения для беспримесной цепочки атомов с массами 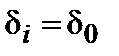 отстоят друг от друга на разных расстояниях
отстоят друг от друга на разных расстояниях  .
. ) атома массы
) атома массы  переменной длины, каждый из которых содержит один атом массы
переменной длины, каждый из которых содержит один атом массы  – матрица переноса для такого отрезка, тогда в периодической цепочке из таких отрезков возникнет запрещенная зона
– матрица переноса для такого отрезка, тогда в периодической цепочке из таких отрезков возникнет запрещенная зона  . Теорема утверждает, что в неупорядоченной цепочке также возникнет запрещенная зона в области
. Теорема утверждает, что в неупорядоченной цепочке также возникнет запрещенная зона в области  , которая является общей для всех областей
, которая является общей для всех областей  . Следовательно, запрещенная зона в спектре рассмотренного ограниченного ансамбля неупорядоченных цепочек может иметь вид как на рис.6.3.
. Следовательно, запрещенная зона в спектре рассмотренного ограниченного ансамбля неупорядоченных цепочек может иметь вид как на рис.6.3. .
.
 должны быть достаточно большими и достаточно сильно отличающимися друг от друга.
должны быть достаточно большими и достаточно сильно отличающимися друг от друга.


