Фазовое представление составляет основу математической теории плотности состояний  для возбуждений в цепочке. По определению
для возбуждений в цепочке. По определению  есть число дозволенных состояний («уровней») в интервале (l, l + d l) в расчете на единичную ячейку цепочки. Сама функция
есть число дозволенных состояний («уровней») в интервале (l, l + d l) в расчете на единичную ячейку цепочки. Сама функция  определяется как предел, к которому стремится распределение уровней для одной цепочки при N ® ¥ или (в неудобных случаях) как среднее по ансамблю таких цепочек.
определяется как предел, к которому стремится распределение уровней для одной цепочки при N ® ¥ или (в неудобных случаях) как среднее по ансамблю таких цепочек.
Как отмечалось, новое стационарное состояние возникает всякий раз, когда фаза  удовлетворяет условию (6.25). Тогда по определению
удовлетворяет условию (6.25). Тогда по определению
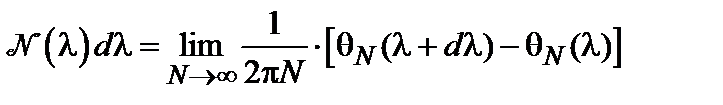 , (6.28-1)
, (6.28-1)
или
 . (6.28-2)
. (6.28-2)
Чтобы избавиться от вычисления производной от функции, которая может и не быть непрерывной, удобно ввести интегральную плотность состояний:
 , (6.29)
, (6.29)
 .
.
Дайсон рассмотрел модель, в которой силовые постоянные  , фигурирующие в уравнении колебаний, подчиняются экспоненциальному или гауссову распределению. В этом случае для интегральной плотности состояний удается получить аналитическое решение. Для простоты изложения опустим выкладки. В результате получается плотность состояний с «хвостом», простирающимся в область, которая в упорядоченной системе была бы запрещена (рис. 6.5).
, фигурирующие в уравнении колебаний, подчиняются экспоненциальному или гауссову распределению. В этом случае для интегральной плотности состояний удается получить аналитическое решение. Для простоты изложения опустим выкладки. В результате получается плотность состояний с «хвостом», простирающимся в область, которая в упорядоченной системе была бы запрещена (рис. 6.5).

Рис.6.5. Интегральная плотность состояний в неупорядоченной цепочке, в которой силовые постоянные распределены по экспоненциальному закону.

 для возбуждений в цепочке. По определению
для возбуждений в цепочке. По определению  есть число дозволенных состояний («уровней») в интервале (l, l + d l) в расчете на единичную ячейку цепочки. Сама функция
есть число дозволенных состояний («уровней») в интервале (l, l + d l) в расчете на единичную ячейку цепочки. Сама функция  удовлетворяет условию (6.25). Тогда по определению
удовлетворяет условию (6.25). Тогда по определению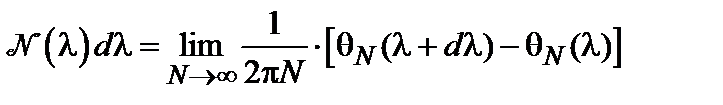 , (6.28-1)
, (6.28-1) . (6.28-2)
. (6.28-2) , (6.29)
, (6.29) .
. , фигурирующие в уравнении колебаний, подчиняются экспоненциальному или гауссову распределению. В этом случае для интегральной плотности состояний удается получить аналитическое решение. Для простоты изложения опустим выкладки. В результате получается плотность состояний с «хвостом», простирающимся в область, которая в упорядоченной системе была бы запрещена (рис. 6.5).
, фигурирующие в уравнении колебаний, подчиняются экспоненциальному или гауссову распределению. В этом случае для интегральной плотности состояний удается получить аналитическое решение. Для простоты изложения опустим выкладки. В результате получается плотность состояний с «хвостом», простирающимся в область, которая в упорядоченной системе была бы запрещена (рис. 6.5).



