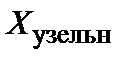Задачи перколяции на регулярных решетках
Пример 1. 137× 137 решетка (Phys.Rev. 1974 Ватсон, Лис) В этом эксперименте определялось при каком количестве светлых узлов прекратится протекание тока по системе.
Рис. 7.3. Схема эксперимента Ватсона и Лиса. а – исходная сетка, количество узлов на рисунке сильно уменьшено; б – кусок сетки с блокированными узлами, блокированные ущлы показаны черными кружками, а неблокированные – светлыми; в – черный узел означает разрыв контакта между четырьмя проволоками, которые связывают узел, светлый узел сохраняет контакт. Через черные узлы электрический ток не течет ни в каком направлении, через светлые узлы ток течет в любом направлении. Значение, вычисленное в результате нескольких испытаний, оказалось равно Можно сделать следующие выводы: - в данной задаче порог был случайной величиной; - необходимо усреднение по реализациям разрезания. - порог зависит от полного числа узлов системе. Если система бесконечна, то предел Рассмотрим это на решетке 2× 2.
Рис. 7.4. Расчет сетки 2× 2. а – исходная сетка; б – блокирован один узел; в, г, д – блокированы два узла. В случае в) ток прерывается после того, как блокирован третий узел, так что Легко понять, что в этой задаче вероятность реализации порога Среднее значение вероятности: Пример 2.Рассмотрим еще одну модель – магнетик. На рис. 69 представлен разбавленный магнетик (атомы со спином будем называть светлыми, а без спинов – темными). Будем называть 2 магнитных атома связанными друг с другом, если они стоят рядом, или если они соединены цепочкой стоящих рядом магнитных атомов.
Рис. 7.5. Кусок плоской решетки с магнитными (светлыми) и немагнитными (темными) атомами. Магнитные атомы образуют один кластер из четырех атомов, один кластер из двух атомов и пять кластеров из одного атома. Границы кластеров показаны штриховыми линиями. Моменты разных кластеров могут быть направлены в разные стороны. В нарисованной реализации системы протекания не будет.
Здесь 1. Существует порог Xc, при котором возникает бесконечный кластер. 2. Предположим, что а) если он темный, то вероятность такого события б) если он светлый, то вокруг него должны быть только темные узлы, т.е. 3. При 4. При 5. При
Рис.7.6. Фрагмент плоской решетки с магнитными (светлые) и немагнитными (темные) атомами в случае большой концентрации магнитных атомов. Все магнитные атомы за исключением атома В принадлежат одному кластеру и имеют одинаковое направление магнитных моментов. 6. В конечной системе четко определенного порога нет. Есть область шириной
Из обобщения результатов численного моделирования на ЭВМ получено, что 7. Порог протекания является самоусредняющейся величиной. 7.3. Перколяция на решетка Бёте Рассмотрим решётку Бёте, она представляет собой искусственную математическую модель, для которой можно получить точное решение. Решётка Бёте представляет собой регулярное дерево, одним из свойств её является то, что веточки связей не пересекаются. P (X) – вероятность принадлежности произвольного узла бесконечному кластеру, т.е. это вероятность прохождения от одного узла к произвольно выбранному другому по неразрушенному пути. Вероятность разрушения пути:
Причин невозможности уйти к бесконечному кластеру из некоторого узла две: 1) Произвольно взятый узел принадлежит к категории темных узлов. Здесь вероятность попасть на темный узел:
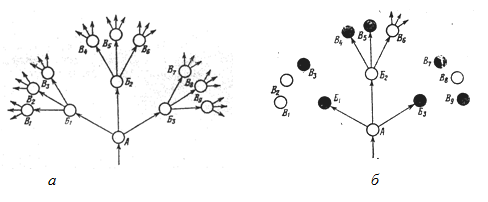
где Х – концентрация светлых (неповрежденных) узлов. Рис. 7.7. Решётка Бёте с координационным числом q = 3. Светлые кружки – категория С, темные – категория Т.
2) Выбранный узел – светлый, но из него нельзя выйти, поскольку далее все каналы прерываются.
где Отметим, что это уравнение всегда имеет одно тривиальное решение Р (Х) = 0 для любого X Рассмотрим решётки Бёте с разными координационными числами. 1. Если q = 1, 2. Если q = 2, 3. Если q
Подставляя это разложение в уравнение (*), получим
Из условия, что на пороге протекания P(X)=0, следует, что порог равен Можно сделать вывод: чем больше веточек (величина q), тем меньше порог, т.е. тем меньше нужно светлых неповрежденных узлов, чтобы образовался бесконечный кластер.
. Рис. 7.8. Качественный вид вероятности образования бесконечного кластера для решетки Бете. 7.4. Регулярные решетки: плоские и пространственные Двумерное пространство можно заполнить квадратной, шестиугольной и треугольной решеткой. Может быть поставлена задача узлов.
Рис. 7.9. Плоские решетки: а – квадратная, б – треугольная, в - шестиугольная.
Можно также поставить задачу связей, где рассматривается разрушение связей по одной.
Рис. 7.10. Фрагмент квадратной решетки с разорванными связями. На рис. 7.10 изображены три кластера из двух связанных узлов (1, 2, 3), один кластер из четырех узлов (4), один кластер из шести узлов (5) и один кластер из десяти узлов (6). Пусть Y – отношение количества правильных узлов к полному числу узлов N, а X – отношение количества правильных связей к полному числу связей M.. Тогда можно показать, что
Смысл этих соотношений нетрудно понять, имея в виду различное число связей у одного узла в квадратной, шестиугольной или треугольной решетках. Значения порогов протекания для плоских решеток приведены в табл. 1. Для квадратной и шестигранной решеток они получены приближенными методами. Все остальные представляют собой результаты точных решений.
Рис. 7.11.. Порог протекания в задаче связей всегда меньше порога протекания задачи узлов.
Рис. 7.12. Функция
Табл.1 Пороги протекания для плоских решеток
Рис.7.13. Функция распределения в задаче о протекании по узлам для решеток различного типа.
|

 .
.
 . Однако, очевидно, что на конечной решетке значение порога – величина случайная. Например, на конечной решетке всегда существует конечная вероятность появления минимального значения порога (для решетки 137× 137
. Однако, очевидно, что на конечной решетке значение порога – величина случайная. Например, на конечной решетке всегда существует конечная вероятность появления минимального значения порога (для решетки 137× 137  ), одна линия осталась неповрежденной.
), одна линия осталась неповрежденной. оказывается достоверной величиной.
оказывается достоверной величиной.
 . В случаях г) и д) ток прерывается после того, как блокирован второй узел, так что
. В случаях г) и д) ток прерывается после того, как блокирован второй узел, так что  . Три случая в), г) и д) равновероятны.
. Три случая в), г) и д) равновероятны. , а
, а  .
. , дисперсия -
, дисперсия -  .
.
 .
. - количество светлых узлов, принадлежащих самому большому кластеру. По определению
- количество светлых узлов, принадлежащих самому большому кластеру. По определению  . Очевидно, что при X = 1 вероятность существования бесконечного кластера равна единице P (1) = 1. При определенной концентрации светлых узлов возникает бесконечный кластер, т.е. существует порог
. Очевидно, что при X = 1 вероятность существования бесконечного кластера равна единице P (1) = 1. При определенной концентрации светлых узлов возникает бесконечный кластер, т.е. существует порог  . Здесь следует отметить несколько моментов.
. Здесь следует отметить несколько моментов. ;
; , здесь z - число ближайших соседей. Полная вероятность события, что данный узел принадлежит бесконечному кластеру:
, здесь z - число ближайших соседей. Полная вероятность события, что данный узел принадлежит бесконечному кластеру: 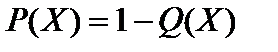 или
или  .
. в системе существуют только конечные кластеры. Бесконечных кластеров нет.
в системе существуют только конечные кластеры. Бесконечных кластеров нет. светлые узлы изолированы. Кратность кластера К» 1.
светлые узлы изолированы. Кратность кластера К» 1. (бесконечная система) справедливо представление о достоверном значении порога протекания, т. е. это значение не зависит от той последовательности, в которой происходит случайная расстановка магнитных и немагнитных атомов (существует маловероятная реализация прямого пути, но вероятность эта крайне мала).
(бесконечная система) справедливо представление о достоверном значении порога протекания, т. е. это значение не зависит от той последовательности, в которой происходит случайная расстановка магнитных и немагнитных атомов (существует маловероятная реализация прямого пути, но вероятность эта крайне мала). , в которую попадают пороги протекания при разных реализациях. Увеличение размеров системы приводит к стягиванию этой критической области в точку.
, в которую попадают пороги протекания при разных реализациях. Увеличение размеров системы приводит к стягиванию этой критической области в точку. .
.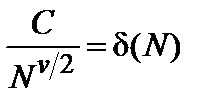 , здесь N - число узлов в системе, ν – индекс радиуса корреляции, С = 0, 54, ν = 1, 3.
, здесь N - число узлов в системе, ν – индекс радиуса корреляции, С = 0, 54, ν = 1, 3.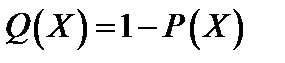 .
. ,
,
 ;
; - вероятность перекрытия всех каналов. Тогда, полная вероятность
- вероятность перекрытия всех каналов. Тогда, полная вероятность  ,
,  ,
, 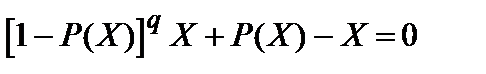 ,
, , т.е. бесконечный кластер в одномерной решётке Бёте не возникает, поскольку один темный узел перекрывает всю цепочку.
, т.е. бесконечный кластер в одномерной решётке Бёте не возникает, поскольку один темный узел перекрывает всю цепочку. и существует второе решение
и существует второе решение  , т.е. Xc = ½.
, т.е. Xc = ½. 2, то существует несколько нетривиальных решений, но для анализа нужно отобрать только действительные корни. Рассмотрим область вблизи порога, т.к. при этом P мало, то справедливо разложение:
2, то существует несколько нетривиальных решений, но для анализа нужно отобрать только действительные корни. Рассмотрим область вблизи порога, т.к. при этом P мало, то справедливо разложение: ,
, ,
, 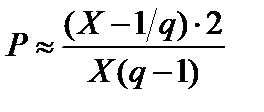
 . Тогда:
. Тогда:  .
.

 . В задаче связей существует также иерархия соотношений:
. В задаче связей существует также иерархия соотношений:
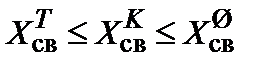


 для задачи связей на двумерной квадратной решетке. 1 – N = 667, 2 – N = 1000, 3 – N = 2000, 4 – N = 6000, 5 – N = ∞.
для задачи связей на двумерной квадратной решетке. 1 – N = 667, 2 – N = 1000, 3 – N = 2000, 4 – N = 6000, 5 – N = ∞.