Структура бесконечного кластера

Модель Шкловского –Де Жена

Рассмотрим задачу узлов допуская, что концентрация неблокированных узлов немного выше пороговой, так что существует бесконечный кластер. Он представляет собой бесконечные цепочки из связанных друг с другом узлов. Если соединить все связанные узлы бесконечного кластера отрезками прямых, то получится набор пересекающихся друг с другом ломаных линий (рис.7.18), где показана одна такая линия).

Структурой бесконечного кластера называют его геометрию в масштабах, гораздо больших, чем период решетки. В таких масштабах изломы, происходящие в отдельных узлах решетки, не воспринимаются глазом и цепочка представляется плавно изогнутой линией.

 

 

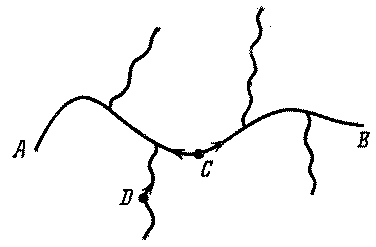
Рис. 7.18. Фрагмент бесконечного кластера с мертвыми концами

 

На рис. 7.18 изображен небольшой фрагмент бесконечного кластера. На концах A и B кластер не кончается – он уходит налево и направо на бесконечное расстояние. Введем теперь следующую классификацию точек и линий бесконечного кластера. Участки бесконечного кластера делятся на скелет и мертвые концы.

Считается, что точка принадлежит скелету бесконечного кластера, если по крайней мере два пути, выходящие из нее в разные стороны, позволяют уйти на бесконечное расстояние. Такой точкой является, например, точка С на рис.90. Из нее можно уйти на бесконечное расстояние, двинувшись и в правую, и в левую стороны. Если только один путь, выходящий из точки, ведет на бесконечное расстояние, то эта точка принадлежит мертвому концу. Например, из точки D на рис. 7.18 можно уйти на бесконечное расстояние, двигаясь только вверх. Движение вниз приводит в тупик. Поэтому считается, что точка D лежит на мертвом конце.

Отбросим мысленно все мертвые концы и постараемся представить как устроен скелет бесконечного кластера. Простейшая модель скелета была предложена независимо друг от друга Б.И. Шкловским и П. де Женом. Для плоской задачи эта модель представляет собой нечто вроде очень большой рыболовной сети, старой и изрядно потрепанной. Она уже потеряла строгую периодичность, ее веревки не натянуты. некоторые узлы в ней порваны, другие съехали со своего места, но тем не менее «в среднем» это сеть (рис.7.19).

 

 

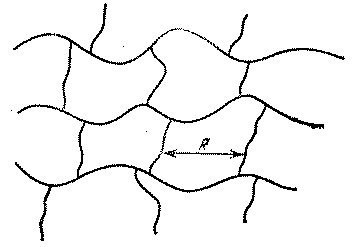
Рис. 7.19. Скелет бесконечного кластера

Характерный линейный размер ячейки этой сети R называется радиусом корреляции бесконечного кластера. Он резко возрастает с приближением к порогу протекания:

. (7.7)

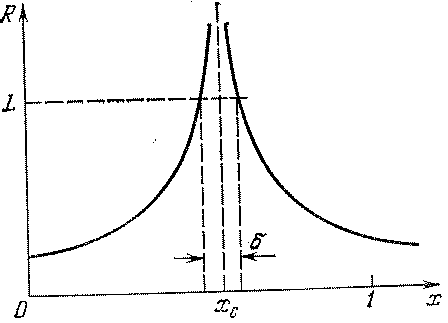
Здесь l – длина, равная по порядку величины периоду решетки, v – положительное число, которое называется индексом радиуса корреляции. Таким образом, по мере приближения к порогу протекания сетка становится все более и более редкой.

Существование обращающегося в бесконечность радиуса корреляции является общим свойством всех критических явлений. То, что он обращается в бесконечность именно но степенному закону (7.7), не является строго доказанным, но лежит в основе современных представлений о критических явлениях и, по-видимому, хорошо подтверждается экспериментальными данными.

Радиус корреляции имеет смысл и при x < x_c, т.е. ниже порога. В этой области он описывает максимальный размер конечных кластеров. Если x → x_c со стороны меньших значений (x < x_c), то радиус корреляции тоже обращается в бесконечность по закону (7.7). Это означает, что при подходе к порогу протекания снизу конечные кластеры неограниченно увеличивают свои размеры и при x = x_c сливаются в бесконечный кластер. Таким образом, зависимость R (x) имеет вид, схематически показанный на рис.7.20.

В случае объемных задач модель Шкловского - де Жена имеет аналогичный вид. Она похожа на сильно испорченный проволочный каркас трехмерной решетки, причем средняя длина одной ячейки выражается формулой (7.7). Следует только иметь в виду, что численные значения индексов радиуса корреляции для плоских и объемных задач разные. Рассмотрим теперь, к каким следствиям приводит представление о сеточной структуре бесконечного кластера.

 

 

Рис. 7.20. Зависимость радиуса корреляции от x. Показана ширина критической области δ для квадрата L × L (см. следующий раздел).