Оценка порога протекания задачи узлов
Разберем теперь схему такого же типа для задачи узлов. Естественно сначала испробовать предыдущий вариант, т.е. посмотреть, как меняется от решетки к решетке величина zx у Легко убедиться, что она меняется почти так же, как каждая из величин z и x у по отдельности. Этому не следует удивляться: в случае задачи связей произведение zx св имеет четкий физический смысл – среднее число целых связей, приходящееся на один узел. В случае задачи узлов связь работает, если она соединяет два белых узла и не работает во всех прочих случаях. Поэтому произведение zx у никакого особого смысла не имеет. Был предложен иной метод оценки порога протекания задачи узлов. Идея состоит в том, чтобы сопоставить каждому узлу определенную долю пространства. После этого Утверждается, что протекание по белым узлам возникает, когда доля пространства, занятая этими узлами, превышает некоторое критическое значение, слабо зависящее от типа решетки. Вообразим вокруг каждого узла решетки шар (или круг в случае плоской решетки) с радиусом, равным половине расстояния до ближайшего соседа. При этом шары (круги), построенные вокруг соседних узлов, касаются друг друга (рис. 7.14). Белому узлу припишем белый шар, а черному узлу – черный. Если два белых узла связаны друг с другом, то между ними есть путь по касающимся друг друга белым шарам (рис. 7.14). Поэтому возникновение протекания означает появление путей бесконечной длины по касающимся друг друга белым шарам. Предположим теперь, что протекание возникает, когда доля полного объема (площади), занимаемая белыми шарами (в плоском случае кругами), превысит некоторое критическое значение, не зависящее от типа решетки. Чтобы проверить это предположение, нужно вычислить доли объема, занимаемые белыми шарами при x = x у, для различных решеток с известным значением x у и сравнить их друг с другом. Сначала необходимо сосчитать долю объема, занимаемого белыми шарами при x = 1, т.е. в случае, когда все шары – белые. Эту величину обозначают буквой f и называют коэффициентом заполнения. Коэффициент заполнения равен доле объема, занятой шарами, построенными вокруг каждого узла решетки и имеющими радиус, равный половине расстояния до ближайшего соседа. Рис. 7.14. Построение касающихся друг друга окружностей в случае шестиугольной решетки. Окружности имеют радиус, равный половине расстояния до ближайшего соседа. Белым узлам соответствует белая, а черным – черная окружности. Пути протекания по белым окружностям показаны жирными линиями.
Коэффициент заполнения существенно зависит от типа решетки, и для каждой решетки его нужно считать отдельно. Чтобы узнать долю объема, заполненного белыми шарами при x < 1, нужно умножить коэффициент заполнения на долю белых шаров, т.е. на x. Таким образом, доля объема, заполненного белыми шарами, равна fx. На пороге протекания она равна fx y. Если предположение об универсальности доли объема, при которой возникает протекание, правильно, то величина fx y должна быть одинаковой для всех решеток. Коэффициенты заполнения для различных решетов даны во втором столбце табл. 7.3. Чтобы представить, как они получены, вычислим величину f для шестиугольной решетки, изображенной на рис.7.14.
Аналогично вычисляются коэффициенты заполнения и для других решеток, причем, как видно из табл. 4, они меняются в широких пределах. Произведения fx y представлены в последнем столбце табл. 3. Видно, что предположение о том, что fx y не зависит от типа решетки, не выполняется точно. Однако и в группе плоских решеток, и в группе объемных решеток это произведение меняется мало.
Таблица 7.4. Произведение f·x yдля разных решеток
Отсюда следует, что с точностью порядка 10 – 15% справедливы формулы: fx y = 0, 5 (7.3) для плоских решеток, и fx y = 0, 16 (7.4) для объемных решеток. Так как вычислить коэффициент заполнения f сравнительно просто, формулы (7.3) и (7.4) дают возможность оценить порог протекания задачи узлов для любой решетки. Легко понять, что критическая доля объема, заполненная белыми шарами, при которой возникает протекание, монотонно уменьшается с увеличением размерности пространства. В одномерном пространстве, т.е. в линейной цепочке узлов, протекание по белым узлам невозможно при сколь угодно малой концентрации черных узлов. Даже один черный узел запирает путь протекания, так как обойти его невозможно. В плоской (двумерной) решетке появляется возможность обхода черных узлов, а в трехмерной (объемной) решетке таких возможностей больше, так как обходные пути не ограничены плоскостью. Идея критического объема оказывается плодотворной не только для решеточных задач. Далее мы столкнемся с задачей, в которой белые и черные шары вообще не находятся в узлах решетки, а просто беспорядочно насыпаны в банку. Нас будет интересовать вопрос о протекании по касающимся друг друга белым шарам. Оказывается, это протекание тоже возникает, когда объем, заполненный белыми шарами, составляет примерно 0, 16 полного объема. Этот результат слабо меняется, если шары отличаются друг от друга радиусом. Может быть рассмотрена задача о пространстве, которое раскрашено случайным образом белой и черной краской. Оказывается, что протекание по областям одного цвета возникает в плоском случае, когда доля поверхности, выкрашенной этим цветом, точно равна 0, 5, а в трехмерном случае, когда доля объема, выкрашенного этим цветом, примерно равна 0, 16. Таблица 7.5
Обобщенные результаты представлены в таблице 5. Существуют некоторые приближенные интегралы, зависящие от типа задачи (задача узлов или задача связей) и от размерности пространства. Значения этих интегралов получены в множестве численных экспериментов: Линейные - Плоские - Объемные - Гипотеза критического объема в задаче узлов позволяет отказаться от регулярности решетки.
|

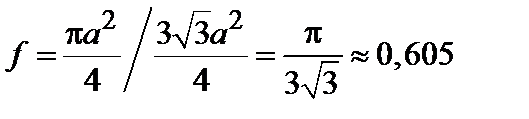 .
.


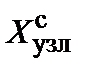


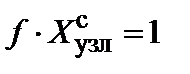 .
.
 (7.5)
(7.5)


