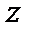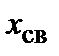Порог протекания для объемных решеток
Задачи связей и узлов ставятся для объемных решеток точно так же, как для плоских. По-прежнему предполагается, что связи имеются только между узлами, являющимися ближайшими соседями. В табл. 7.2 дана сводка порогов протекания задач узлов и связей для описанных выше объемных решеток. Как уже говорилось, в трехмерном случае не существует ни одного точного решения. Все результаты, приведенные в табл. 7.2 получены различными приближенными методами, как правило, использующими ЭВМ.
Табл. 7.2 Пороги протекания для объемных решеток
Задача состоит в том, чтобы используя данные табл.7.1 и 7.2 понять, почему для одних решеток пороги протекания сравнительно большие, а для других – маленькие. Начнем с задачи связей. Если все связи – целые, то каждый узел связан с z другими узлами, где число ближайших соседей z сильно меняется от решетки к решетке. При заданной доле целых связей x каждый узел в среднем связан с zx другими узлами. Попробуем проверить следующую гипотезу: может ли величина zx, представляющая среднее число узлов, с которыми связан каждый узел, содержать информацию, достаточную для определения наличия в решетке протекания. Возможно, что никакой другой информации о свойствах решетки, кроме числа z, и не надо, и протекание возникает у всех решеток при одном и том же значении величины zx? Ясно, что эта гипотеза не может быть точной. Но может быть, она справедлива приближенно? Проверить это очень просто. Нужно для всех решеток с известными порогами протекания задачи связей вычислить произведение zx св. Если оно окажется универсальным, т.е. одинаковым для всех решеток или хотя бы приближенно одинаковым, значит, высказанная гипотеза верна или верна приближенно. Соответствующие данные собраны в табл. 3. Видно, что с погрешностью меньше чем 10%, для плоских решеток справедлива формула:
а для объемных решеток –
Таким образом, гипотеза об универсальности среднего числа связей на узел, требуемого для возникновения протекания, не является точной, но приближенно выполняется. Если принять во внимание, что как в группе плоских решеток, так и в группе объемных решеток каждая из величин z и x св меняется но крайней мере в два раза, то точность, с которой в каждой группе величина zx св постоянна, следует признать высокой.
Табл.3 Произведение
Итак, чтобы приближенно оценить порог протекания задачи связей, достаточно знать число ближайших соседей и воспользоваться формулой (7.1) в случае плоских решеток и формулой (7.2) в случае объемных решеток. Порог протекания задачи связей наиболее чувствителен к числу ближайших соседей и значительно менее чувствителен ко всем прочим свойствам решеток (например, к числу вторых соседей, т.е. соседей, следующих по удаленности от данного узла). Таким образом, мы получили очень простой и относительно точный способ оценки порогов протекания задачи связей, пригодный для любой решетки.
|

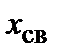
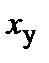
 , (7.1)
, (7.1)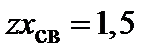 . (7.2)
. (7.2)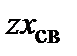 для разных решеток
для разных решеток