Задача координационных сфер
Обобщение состоит в том, что связь распространяется на узлы, расположенные не только в первой координационной сфере. Результаты были получены только путем расчетов на ЭВМ.
Рис.7.15. Путь протекания по охватывающим окружностям, построенным на квадратной решетке. Взаимодействие учитывается на расстоянии втрое большем, чем между ближайшими соседями. Путь протекания показан ломаной линией.
Таблица 7.6. Пороги протекания для плоских решеток
Эти результаты могут быть обобщены на случай
Таблица 7.7. Пороги протекания для объемных решеток
Примечание: (*) - все 3 сферы используются для связи, следовательно число связей увеличивается. В случае объемных решеток все также может быть обобщено для Рассмотрим задачу о вложенных сферах
где R – радиус сфер, N – плотность центров в единице объема Смысл соотношения в следующем: число центров, попадающих в зону влияния должны достичь определенного значения (конкретно 2, 7).
Рис. 7.16. Пути протекания по охватывающим окружностям (показаны ломаными линиями, точки – центры окружностей)
Сделаем следующие обобщения. 1) в случае произвольной формы вложенных объектов
Условие образования бесконечного кластера выполняется с хорошей точностью. Можно, например, заменить сферу на овал. Оказывается, интеграл сохраняется для всех выпуклых фигур. Существенным является критическое заполнение объема, а чем – не важно. Как только концентрация достигнет критической величины для объектов данного размера, тогда появится протекание. 2) Можно ввести понятие касающихся сфер (или проводимость по белым сферам, а черные сферы того же радиуса – диэлектрики)
Рис. 7.17. Смесь проводящих и непроводящих частиц
Для касающихся сфер критическим условием является следующее:
Пример физической задачи Наличие примеси создает в запрещенной зоне полупроводника локализованные состояния. Как отмечалось, если атом помещается в среду с диэлектрической проницаемостью
т.е. электрон примесного атома в среде имеет большой радиус орбиты и небольшую энергию связи. При введении примесей, они распределяются хаотически. Однако, эксперимент показывает, что при увеличении концентрации примесей происходит переход к металлической проводимости, т.е. имеет место переход диэлектрик – металл. Покажем, что в определенных условиях это т переход соответствует образованию связанных примесей и создание бесконечного кластера. По бесконечному кластеру примесей возможна проводимость. Действительно, эксперимент показал, что переход происходит при выполнении условия Пусть Концентрация примеси является заданной ((7.6), где N -задано). Далее, пусть
тогда, после подстановки На этих " хвостах" волновых функций происходит перекрытие и образование бесконечного кластера.
|




 . А именно:
. А именно:  - условие на порог протекания. Если R увеличится, следовательно нужна меньшая плотность окружностей, что бы реализовать протекание (n – средняя плотность в единицу площади поверхности).
- условие на порог протекания. Если R увеличится, следовательно нужна меньшая плотность окружностей, что бы реализовать протекание (n – средняя плотность в единицу площади поверхности).
 .
. 
 , (7.6)
, (7.6) , следовательно
, следовательно  = 2, 7.
= 2, 7.
 . Если эффективный объем проводящих шаров ~0, 16, возникает бесконечный кластер.
. Если эффективный объем проводящих шаров ~0, 16, возникает бесконечный кластер. , то его боровский радиус:
, то его боровский радиус: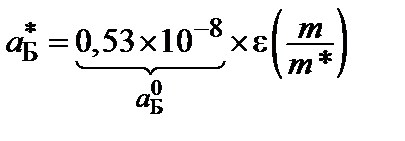 , где e» 10 ¸ 15, m *» 0.1me
, где e» 10 ¸ 15, m *» 0.1me .
. = 0, 02, где
= 0, 02, где  – эффективный объем, занимаемый волновой функцией примеси.
– эффективный объем, занимаемый волновой функцией примеси. - волновая функция S-типа, где
- волновая функция S-типа, где  - большое.
- большое. - необходимый эффективный радиус перекрытия волновых функций примесных атомов, достаточный для переходов электрона с атома на атом, тем самым, создающих бесконечный кластер. Пусть выполняется соотношение критического условия для трехмерного случай перекрывающихся сфер.
- необходимый эффективный радиус перекрытия волновых функций примесных атомов, достаточный для переходов электрона с атома на атом, тем самым, создающих бесконечный кластер. Пусть выполняется соотношение критического условия для трехмерного случай перекрывающихся сфер. ,
, = 10 ÷ 15,
= 10 ÷ 15,  можно найти параметр перекрытия " хвостов" волновых функций
можно найти параметр перекрытия " хвостов" волновых функций  .
.


