Мощность скелета бесконечного кластера вблизи порога протекания. Роль мертвых концов
Как и электропроводность, функция P (x), представляющая долю узлов, принадлежащих бесконечному кластеру, обращается в нуль при x = xc. Исследования показали, что вблизи порога эта функция имеет вид
где D – численный коэффициент порядка единицы, а В функцию P (x) дают вклад все узлы бесконечного кластера – и принадлежащие скелету, и принадлежащие мертвым концам. С помощью модели бесконечного кластера можно определить, каких узлов больше. Допустим сначала, что мертвых концов совсем нет, и вычислим вклад в P (x) от скелета бесконечного кластера. В двумерном случае на каждую ячейку бесконечного кластера приходится порядка R / a узлов, принадлежащих скелету, где a – период решетки (как и в предыдущем разделе, здесь делается оценка, не претендующая на установление численных коэффициентов). Площадь ячейки порядка
Здесь знак «~» означает равенство по порядку величины (без учета численных коэффициентов порядка единицы). В трехмерном случае на каждую ячейку бесконечного кластера тоже приходится (R / a) узлов, принадлежащих скелету, но полное число узлов в ячейке порядка (R / a)3. Поэтому в трехмерном случае
Сравнивая формулы (7.16) и (7.17) с формулами (7.12) и (7.14), можно видеть, что доля узлов, принадлежащих скелету бесконечного кластера, по порядку величины совпадает с функцией Сравнивая (7.16) и (7.17) с формулой (7.15), видим, что
в двумерном случае, а в трехмерном случае
Вспомним, что
|

 , (7.15)
, (7.15) – еще один критический индекс. Установлено, что для двумерных задач
– еще один критический индекс. Установлено, что для двумерных задач  , а для трехмерных
, а для трехмерных  . Эти результаты получены главным образом с помощью ЭВМ.
. Эти результаты получены главным образом с помощью ЭВМ. и, следовательно, полное число всех узлов в ячейке порядка
и, следовательно, полное число всех узлов в ячейке порядка  . Отсюда следует, что доля узлов, принадлежащих скелету бесконечного кластера,
. Отсюда следует, что доля узлов, принадлежащих скелету бесконечного кластера, . (7.16)
. (7.16) . (7.17)
. (7.17) .
.
 .
.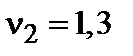 , а
, а  . Следовательно,
. Следовательно,  , a
, a  . Таким образом, и в двумерном, и в трехмерном случаях отношение
. Таким образом, и в двумерном, и в трехмерном случаях отношение 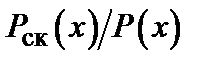 быстро стремится к нулю при x → xc. Это значит, что узлы, образующие скелет бесконечного кластера, составляют ничтожную долю от полного числа узлов, принадлежащих бесконечному кластеру. Основная «масса» бесконечного кластера сосредоточена в мертвых концах и совершенно бесполезна с точки зрения электропроводности. Поэтому вблизи порога протекания
быстро стремится к нулю при x → xc. Это значит, что узлы, образующие скелет бесконечного кластера, составляют ничтожную долю от полного числа узлов, принадлежащих бесконечному кластеру. Основная «масса» бесконечного кластера сосредоточена в мертвых концах и совершенно бесполезна с точки зрения электропроводности. Поэтому вблизи порога протекания  . Однако именно мертвые концы определяют спонтанную намагниченность ферромагнетика с примесями вблизи порога протекания.
. Однако именно мертвые концы определяют спонтанную намагниченность ферромагнетика с примесями вблизи порога протекания.


