Концентрационная зависимость прыжковой проводимостиДля третьего интервала температур проводимость имеет вид
т.е. это термоактивированная проводимость. Предэкпоненциальный множитель Данный i -й узел связан со всеми другими узлами j, находящимися внутри сферы некоторого радиуса R, описанной вокруг i -го узла. При некотором R = Rc , как следует из задачи о вложенных сферах (рис.88), будет образовываться бесконечный кластер, в котором каждый следующий узел лежит внутри сферы, описанной вокруг предыдущего. Тогда критическое значение параметра x определяется через критический радиус как
Отсюда
где Способы проверки: 1. ЭВМ и использование 1-ого и 2-ого законов Кирхгофа, точное решение для сопротивления 2. Экспериментальные результаты для p -Ge – германиевый полупроводник р -типа. Здесь задача является частично перколяционной, связаны те узлы, которые попадают в область влияния другого узла.
|
,
имеет сильную концентрационную зависимость. Для данной температурной области характерно то, что Т относительно велика, т.е. всегда можно найти фонон для прыжка 
. Следовательно, основной вклад связан со слагаемым 
.
. Результат задачи о вложенных сферах: 
, т.е. в радиусе влияния 
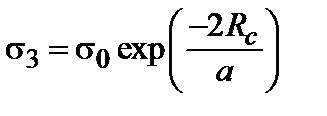должно быть 2, 75 соседей, или
.
или 
,
.
, где 
– случайная величина и разбросана в широком интервале, дает практическое совпадение результатов.
