Узкие зоны и переход Мотта
Из предыдущего ясно, что задачи типа Кронига-Пенни не описывают переход локализация – делокализация. Действительно, допустим, что примесные атомы располагаются периодически в матрице основного материала. Матрица A имеет период решетки а, и в нее мы внедрили примеси со своей решеткой B, обладающей периодом b. Потенциал примесной подрешетки можно записать как
где суммирование идет по узлам подрешетки B. Пусть известны волновые функции
Мы учли потенциал матрицы A, введя эффективную массу носителей m*. Действительно, если атом помещается в среду с диэлектрической проницаемостью ε, то его боровский радиус увеличивается в сотни раз
где e» 10 ¸ 15, m *» 0, 1 me. Ограничимся случаем, когда состояния n невырождены. Для простоты будем считать, что W, ширина примесной зоны, меньше расстояния между Искомая волновая функция является решением электронной задачи для подрешетки B
и конструируется из волновых функций для примесного атома (9.1)
Такое стандартное разложение по атомным волновым функциям Значение коэффициентов aj следует искать из принципа минимума полной энергии E. Отметим, что среднее значение энергии не является квадратичной формой коэффициентов aj, т.к.
Подставляя
Учитывая, что
В силу трансляционной симметрии подрешетки В:
где
Выделяя (9.2) слагаемое с m = 0, получим
Очевидно, что
Тогда, в приближении ближайших соседей по подрешетке В (кубической), получим известный результат приближения сильной связи:
т.е. ширина подзоны
Введем обозначение Величина m ** играет роль эффективной массы электронов в образовавшейся энергетической зоне для примесной подрешетки B. С ростом периода этой подрешетки b 0 эффективная масса m ** экспоненциально растет. Действительно,
При этом, каким бы большим не было b 0, состояние электрона в этой примесной зоне является модулированной плоской волной, и электрон остается делокализованым. Отметим, что зона, образованная примесями, заполнена не более чем наполовину, поскольку каждая примесь дает (или забирает) один электрон, а каждый уровень дважды вырожден по спину. Таким образом, получается, что, если примеси действительно расположены периодически, то проводимость электронов в этой зоне металлическая при сколь угодно малой концентрации примесей. Заметим, что при увеличении b 0 ширина зоны будет уменьшаться
и задача рассматривается как одноэлектронная для примесного центра. Именно в этом причина противоречия с вопросом о делокализации. Одноэлектронное приближение хорошо работает при расчете широких зон металлов и оказывается недопустимым в случае узких зон. Уже отмечалось, что волновая функция электрона Y вблизи каждого j -го узла слабо отличается от узельной j j. Оценим ситуацию, когда на одном примесном центре находятся два электрона. Энергия такого состояния порядка Если эта энергия меньше ширины зоны, т.е.
то перестройка волновой функции связанная с взаимодействием электронов незначительна (так обстоит в хороших металлах). В нашем случае? При больших значениях b0
Пусть b 0 велико. На каждом узле примесной подрешетки разрешены два уровня Рис. 9.1. Электронные зоны в зависимости от периода примесной подрешетки b 0. Слева от точки А – диэлектрик, справа – металл При конечном значении b 0оба уровня расплываются в зону шириной порядка I (b 0). В всех зонах может быть не более N электронов, поскольку, например, в нижней зоне на одном узле не может быть двух электронов. Таким образом, при достаточно больших расстояниях между примесями b 0 нижняя зона должна быть полностью заполнена, а верхняя – пуста. При некотором значении b 0, которое определяется условием I ( Существует переход в регулярной системе от локализованного состояния в делокализованное. Это переход Мотта. Более последовательное изучение такого перехода может быть проведено в модели Хаббарада. Действительно, в рамках этого приближения два электрона со спином s, находящиеся на одном узле, отталкиваются. Система описывается уравнением:
где Модель Хаббарда допускает аналитическое решение только в одномерном случае. Результатом этого решения является щель между верхней и нижней зоной, которое сохраняется при любых значениях отношения I (b 0)/ U 0, т.е. в одномерном случае всегда система является изолятором. В двух и трехмерном случаях возможны численные решения, из которых следует качественный результат, полученный выше.
|

 ,
, и энергии
и энергии  электронов на одном примесном атоме, находящемся в матрице.
электронов на одном примесном атоме, находящемся в матрице. . (9.1)
. (9.1) ,
, .
. .
.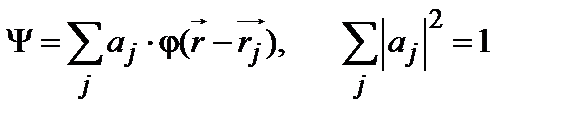
 должно быть хорошим приближением, если радиус локализации волновых функций j мал по сравнению с периодом подрешетки В – b 0. Действительно, основной вклад в энергию дают области пространства, в которых волновая функция Y велика, т.е. в сфере действия одного из примесных центров (т.е. там, где и «работает» уравнение (1)).
должно быть хорошим приближением, если радиус локализации волновых функций j мал по сравнению с периодом подрешетки В – b 0. Действительно, основной вклад в энергию дают области пространства, в которых волновая функция Y велика, т.е. в сфере действия одного из примесных центров (т.е. там, где и «работает» уравнение (1)). , соответствующие разным узлам, неортогональны.
, соответствующие разным узлам, неортогональны. .
. и
и  , с условием нормировки получим (как в методе сильной связи):
, с условием нормировки получим (как в методе сильной связи):
 – число узлов подрешетки B, получим
– число узлов подрешетки B, получим .
.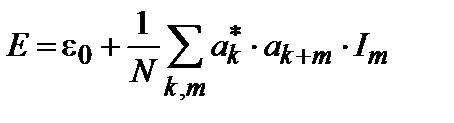 , (9.2)
, (9.2) – уровень примесного атома в матрице,
– уровень примесного атома в матрице,  – энергетический интеграл перекрытия
– энергетический интеграл перекрытия .
. .
. (предполагаем, что волновая функция примесного атома имеет простейший вид
(предполагаем, что волновая функция примесного атома имеет простейший вид  ). Можно показать, что набор ak минимизирует значение энергии, если коэффициенты имеют вид
). Можно показать, что набор ak минимизирует значение энергии, если коэффициенты имеют вид .
. ,
, . В частности для простой кубической решетки, где z = 6 и для малых k
. В частности для простой кубической решетки, где z = 6 и для малых k .
.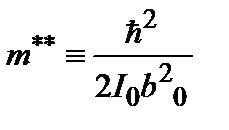 , тогда
, тогда 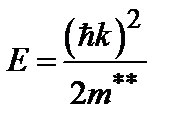 .
. . (9.3)
. (9.3) , (9.4)
, (9.4) эВ, боровский радиус:
эВ, боровский радиус:  .
. ,
, .
. и
и  . Если на узле один электрон, то из этих двух уровней будет заполнен только нижний.
. Если на узле один электрон, то из этих двух уровней будет заполнен только нижний. )» U 0, верхняя граница нижней зоны пересечет нижнюю границу верхней. Качественно, до этой точки система будет изолятором, после нее – металлом.
)» U 0, верхняя граница нижней зоны пересечет нижнюю границу верхней. Качественно, до этой точки система будет изолятором, после нее – металлом. ,
, - оператор заполнения состояния на j -м уровне со спином s. Последнее слагаемое описывает отталкивание электронов, имеющих разный спин и находящихся на одном узле.
- оператор заполнения состояния на j -м уровне со спином s. Последнее слагаемое описывает отталкивание электронов, имеющих разный спин и находящихся на одном узле.


