Кулоновская блокада и переход металл-изолятор
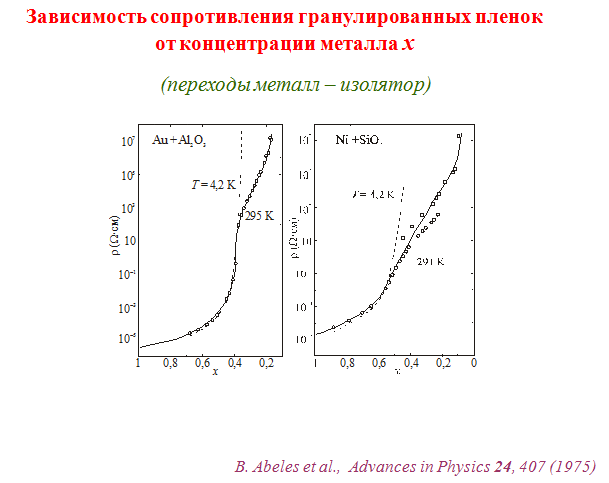
На рис.5(a) приведены зависимости сопротивления от относительной концентрации металла в керметах системы Au+Al2O3 (рис.10.2), измеренные при двух существенно разных температурах. На графике явно видны две области концентраций x. Область
Рис. 10.5. Переход металл-изолятор. Зависимость сопротивления гранулированных пленок от концентрации металла x . Обратите внимание на шкалу на оси ординат: диапазон изменения сопротивления больше 12 порядков. B. Abeles et al., Advances in Physics 24, 407 (1975)
Аналогичный график Стандартное описание в терминах перколяционной модели предполагает, что при концентрациях x > xc линии тока целиком проходят внутри металлического кластера, а при x < xc ток должен хотя бы частично проходить через изолятор. Тогда температурную зависимость
надежно отличая ее и от
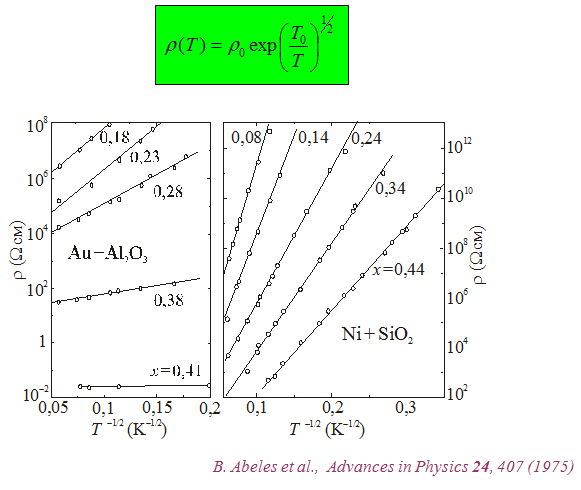
Рис.10.6. Температурная зависимость удельного сопротивления гранулированных систем. B. Abeles et al., Advances in Physics 24, 407 (1975) Функциональной зависимости (4) нет у соответствующих массивных изоляторов, ни у Al2O3, ни у SiO2. К тому же наклон прямых на рис.6, определяемый величиной Теоретическая модель исходит из двух фундаментальных предположений: 1. Между соседними гранулами возможно туннелирование. Здесь теряется инвариантность относительно масштаба решетки, характерная для перколяционных задач, и исключаются системы типа совокупности металлических шариков от подшипников. Не обязательно, чтобы из каждой гранулы было возможно туннелирование во все соседние гранулы. Точнее можно сказать так: совокупность гранул, между которыми возможен обмен носителями посредством туннелирования, должна представлять собой развитый бесконечный кластер. Это предположение определяет то, что обычно называют подвижностью носителей
где 2. Каждая заряженная металлическая гранула создает электрическое поле в зазоре между собой и соседними гранулами, являясь таким образом обкладкой локального микроконденсатора. Емкость такого конденсатора порядка произведения радиуса гранулы
Если заряд в конденсаторе q, то энергия поля в нем
Заметьте: Материал остается при этом электрически нейтральным, поскольку число электронов и дырок (положительно и отрицательно заряженных гранул) примерно одинаково. Энергия и тех и других отсчитывается от уровня Ферми. Энергия
может определять и свойства материала как целого.
Поскольку в показателе экспоненты в выражении (10.9) имеется два слагаемых и длина a в одном из них входит в числитель, а в другом в знаменатель, существует значение
при котором показатель имеет минимум. Значение длины a в реальном материале наверняка имеет дисперсию. Существование минимума означает, что ток в основном будет идти вдоль цепочек из гранул с выделенным значением
Прежде, чем обсуждать полученный результат, следует сделать существенную оговорку. Длина a в формулах (10.5) и (10.7) имеет разный смысл: это зазор между гранулами в (5) и размер гранул в (10.7)). На фотографиях на рис.10.1, 2, 3 видно, что они не равны. Но вместо фактически сделанного предположения об их равенстве можно ограничиться гораздо более реалистичным предположением об их пропорциональности. Это означает, что различные участки после масштабирования становятся статистически одинаковыми. В такой модели основной вывод останется прежним, лишь в выражении (10.11) появится в качестве дополнительного множителя корень из коэффициента пропорциональности. Более того, основной вывод сохранится при любой функциональной связи при данном x между размерами гранул a и зазорами a' между ними; лишь бы эти две величины не были статистически независимыми. Итак, выясняется, что при низких концентрациях металлической фазы x < xc ток течет по гранулированному материалу неравномерно, концентрируясь в областях с оптимальным средним размером гранул. Этот оптимальный размер зависит от температуры. Поэтому при изменении температуры распределение тока по материалу должно меняться. Сравните туннельную проводимость в гранулированной системе с прыжковой проводимостью при наличии кулоновской щели. Одинаковая функциональная зависимость Сходство между этими двумя задачами не случайно. Если устремить размер гранул к нулю, то они превратятся в примесные центры, которые могут быть либо заряжены, либо электронейтральны. При таком предельном переходе одна задача должна естественно перейти в другую. Но в изоляторе с примесными центрами есть кулоновская щель, а в металле с большим количеством примесей из-за кулоновского электрон-электронного взаимодействия появляется минимум плотности состояний на ферми-уровне. Чего-то аналогичного следует ожидать и в гранулированном материале. Справедливость этих ожиданий демонстрирует туннельный эксперимент.
Рис.10.7 Туннельные характеристики системы Al-Al2O3- (Ni+SiO2). B. Abeles et al., Advances in Physics 24, 407 (1975) В эксперименте были использованы пленки толщиной 100Å;. Поскольку при всех значениях характерные размеры металлических гранул были меньше 50Å;, с точки зрения процессов, формирующих электронный спектр, пленка Ni+SiO2 представляет собой трехмерную структуру. Плоскость контакта является ее срезом. Процесс туннелирования может происходить только в выходяшие на плоскость контакта металлические гранулы. Они занимают на этой плоскости ту же долю x, что и в объеме. При больших значениях x, а именно уже при x=0.66 (верхняя кривая), наличие диэлектрических вкраплений несущественно, Ni+SiO2 ведет себя как обычный металл, а структура на кривой Таким образом, хотя туннелирование происходит в отдельные гранулы, извлекаемая из эксперимента функция В [2] детально рассмотрен вопрос об обработке данных представленных на рис.10.7 и показано, что при исчезновении бесконечного кластера, когда происходит перколяционный переход и доля p принадлежащая бесконечному кластеру обращается в нуль, становится нулем и плотность состояний на ферми-уровне.
то гранулярность становится несущественной. Важно, конечно, чтобы не было слишком большим (как в системе из шариков от подшипников), иначе окрестность перехода станет нереализуемо малой.
СПИСОК ЛИТЕРАТУРЫ
1. Займан Дж. - Модели беспорядка: теоретическая физика однородно неупорядоченных систем; Пер.с англ. - М.: Мир, 1982. - 592 с. 2. Гантмахер В. Ф. - Электроны в неупорядоченных средах - М.: Физматлит, 2005. - 232 с. 3. Эфрос А.Л. Физика и геометрия беспорядка. М.: Наука, 1982. 4. Бонч-Бруевич В.Л. и др. Электронная теория неупорядоченных полупроводников. М.: Наука, 1981. 5. Комник Ю.Ф. Физика металлических пленок. М.: Атомиздат, 1979. 6. Б.И.Шкловский, А.Л.Эфрос, Электронные свойства легированных полупроводников. М.: Наука, 1979. - 416 с.
|

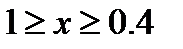 является металлической: сопротивление
является металлической: сопротивление  сравнительно мало, сравнительно слабо зависит от температуры и постепенно растет с уменьшением x; где-то вблизи значения
сравнительно мало, сравнительно слабо зависит от температуры и постепенно растет с уменьшением x; где-то вблизи значения 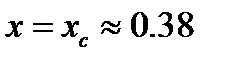 находится граница двух областей; наконец, для диэлектрической области характерен очень резкий рост сопротивления с уменьшением x и очень сильная температурная зависимость
находится граница двух областей; наконец, для диэлектрической области характерен очень резкий рост сопротивления с уменьшением x и очень сильная температурная зависимость 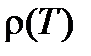 .
.
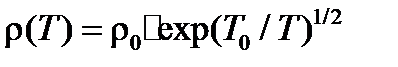 (10.4)
(10.4)
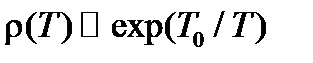 , и от
, и от 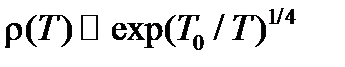 .
.
 , зависит от величины x. Следовательно, транспорт в обсуждаемых материалах контролируется не только изолятором, но и металлическими гранулами. Это и есть тот экспериментальный факт, который необходимо осмыслить и объяснить.
, зависит от величины x. Следовательно, транспорт в обсуждаемых материалах контролируется не только изолятором, но и металлическими гранулами. Это и есть тот экспериментальный факт, который необходимо осмыслить и объяснить. ; здесь под
; здесь под 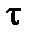 следует понимать время, за которое происходит туннелирование заряда
следует понимать время, за которое происходит туннелирование заряда  с эффективной массой
с эффективной массой 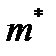 . Действительно, раз туннелирование это основной механизм передвижения зарядов в пространстве, то подвижность зарядов пропорциональна вероятности туннелирования
. Действительно, раз туннелирование это основной механизм передвижения зарядов в пространстве, то подвижность зарядов пропорциональна вероятности туннелирования (10.5)
(10.5)
 и
и  - ширина и высота барьера.
- ширина и высота барьера. на диэлектрическую проницаемость
на диэлектрическую проницаемость 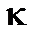 окружающего его изолятора (емкость уединенного шара),
окружающего его изолятора (емкость уединенного шара),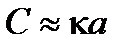 (10.6)
(10.6)
 . Поэтому для размещения на грануле одного избыточного электрона, q=e, требуется кулоновская энергия
. Поэтому для размещения на грануле одного избыточного электрона, q=e, требуется кулоновская энергия 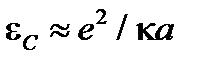 . Отсюда следует, что концентрация зарядов пропорциональна
. Отсюда следует, что концентрация зарядов пропорциональна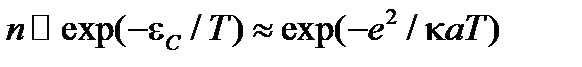 (10.7)
(10.7)
 отнюдь не мала. Для гранулы размером 50Å; при
отнюдь не мала. Для гранулы размером 50Å; при 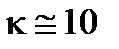 она порядка 300K. Это означает, что при низких температурах туннелирующих носителей экспоненциально мало. Именно это обстоятельство лимитирует проводимость. Отсюда название кулоновская блокада. Оно употребляется чаще применительно к изолированыым наноструктурам, таким, как пары туннельных контактов малой емкости, когда величина
она порядка 300K. Это означает, что при низких температурах туннелирующих носителей экспоненциально мало. Именно это обстоятельство лимитирует проводимость. Отсюда название кулоновская блокада. Оно употребляется чаще применительно к изолированыым наноструктурам, таким, как пары туннельных контактов малой емкости, когда величина 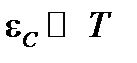 (10.8)
(10.8)
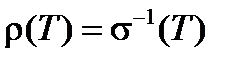 . Поскольку проводимость s пропорциональна произведению концентрации на подвижность, получаем
. Поскольку проводимость s пропорциональна произведению концентрации на подвижность, получаем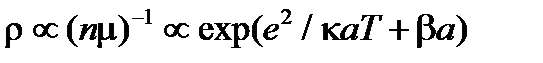 (10.9)
(10.9)
 (10.10)
(10.10)
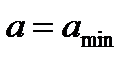 , а сопротивление материала будет описываться формулой (10.4) со значением T0.
, а сопротивление материала будет описываться формулой (10.4) со значением T0. (10.11)
(10.11)
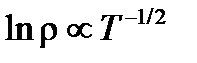 , одно и то же исходное взаимодействие - кулоновское, схожие механизмы смены с температурой основных тунннельных (токовых) путей.
, одно и то же исходное взаимодействие - кулоновское, схожие механизмы смены с температурой основных тунннельных (токовых) путей.
 появляется из-за сверхпроводимости контрэлектрода Al. Изменения в кривых при меньших полностью контролируются гранулированным электродом, поскольку с Al ничего не происходит. Абстрагируясь от его неоднородности, можно извлечь из каждой экспериментальной кривой функцию плотности числа состояний для гранулированного электрода. Результат представлен на рис.7(b).
появляется из-за сверхпроводимости контрэлектрода Al. Изменения в кривых при меньших полностью контролируются гранулированным электродом, поскольку с Al ничего не происходит. Абстрагируясь от его неоднородности, можно извлечь из каждой экспериментальной кривой функцию плотности числа состояний для гранулированного электрода. Результат представлен на рис.7(b).  на ферми-уровне, который превращается в мягкую щель. Согласно рис.10.7, критическое значение управляющего параметра в системе Ni+SiO2 равно xс=0.56. То же значение получается и из кривых рис.5(b): именно при этом x меняет знак производная
на ферми-уровне, который превращается в мягкую щель. Согласно рис.10.7, критическое значение управляющего параметра в системе Ni+SiO2 равно xс=0.56. То же значение получается и из кривых рис.5(b): именно при этом x меняет знак производная 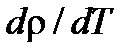 .
. (10.12)
(10.12)



