ТЕОРИЯ ПРЫЖКОВОЙ ПРОВОДИМОСТИ
Прыжковой проводимостью называют перенос тока за счет перескоков носителей между локализованными состояниями. Это явление можно наблюдать в полупроводниках с примесями и в аморфных телах, в которых она существует в большом температурном интервале (0 ÷ 10 К), в полупроводниках этот температурный интервал – (0 ÷ 1 К). Ранее мы рассматривали 4 температурных интервала проводимости полупроводников. 1. В чистом полупроводнике с запрещенной зоной 2. При комнатной температуре и более низких температурах (T < <
где Если концентрация примесей мала
где Проводимость таких слаболегированных систем осуществляется за счет заброса электрона в зону проводимости (рис.8.1).
Рис.8.1. Проводимость за счет заброса электронов в зону проводимости.
3. При температурах T < < E 2 такие процессы «вымораживаются» и существенным становится вклад от прыжков электронов по примесям, за счет малого конечного перекрытия волновых функций примесных состояний. Здесь Следует помнить, что необходимым условием прыжка является наличие свободных мест на донорах (два электрона на узле - невыгодно). При низких температурах это можно обеспечить только компенсацией полупроводника, т.е. присутствием некоторой части неосновных примесей (например, акцепторов).
Рис. 8.2. Прыжки электронов по примесям, за счет малого конечного перекрытия волновых функций примесных состояний.
В результате: - возникает переход части электронов с донорных примесей на акцепторные и освождение части мест на первых; - появление положительно заряженных донорных примесей и отрицательно заряженных акцепторных. Второй фактор, в силу дальнодействия кулоновских полей и хаотичного расположения в пространстве как тех, так и других, приводит к возникновению флуктуирующего в пространстве потенциала для донорных уровней. Создается разброс этих уровней по энергии, который значительно превышает малое расщепление уровней соседних доноров, связанное с перекрытием волновых функций. Этот факт препятствует делокализации донорных электронов по примесям и приводит к локализации состояния на отдельных донорах. Вследствие разброса уровней по энергии нужен захват или испускание фонона для перескока. Этот факт отражается в выражении
Рис. 8.3. Энергетические схему слабо- и сильнокомпенсированных полупроводников в пренебрежении крупномасштабным потенциальным рельефом. Сплошная линия – зона проводимости, штрих-пунктирная – уровень Ферми. Короткие черточки изображают уровни доноров, а темные кружки – занимающие их электроны. Справа изображена плотность состояний на донорных уровнях. Заполненные состояние заштрихованы. Валентная зона и акцепторные уровни не показаны.
На рис 8.5 представлена зависимость удельного сопротивления от обратной температуры для Ge p -типа со степенью компенсации К = 0, 4. для различных значений концентраций примесей. Характерно, что при изменении концентрация увеличивается в 2 раза, а сопротивление изменилось в 100 раз. Концентрация N уменьшается, следовательно расстояние между примесями в среднем увеличивается, значит интеграл перекрытия экспоненциально уменьшается. Тогда вероятность перескока падает, а сопротивление растет.
Рис. 8.5. Зависимость удельного сопротивления от температуры для Ge p -типа со степенью компенсации К = 0, 4. Концентрация акцепторов 1 – 11 равны (в см -3): 1 – 7, 5·1014; 2 – 1, 4·1015; 3 – 1, 5·1015; 4 – 2, 66·1015; 5 – 3, 6·1015; 6 – 4, 8·1015; 7 – 7, 2·1015; 8 – 9, 0·1015; 9 – 1, 4·1016; 10 – 2, 4·1016; 11 – 3, 5·1016.
4. В аморфных полупроводниках об электронных состояниях, по которым происходят прыжки, известно значительно меньше, чем в кристаллических. Эти состояния связаны не с примесями, а с флуктуациями структуры и стехиометрического состава. Но и для аморфных, и для кристаллических конденсированных тел при температурах T < 1 K возникает зависимость вида
Мы покажем, что области (3), (4) могут быть описаны в рамках перколяции.
|

 удельная электропроводимость
удельная электропроводимость  , что означает заброс через зону.
, что означает заброс через зону. ,
, 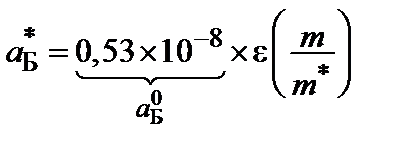 ,
, ,
,  .
. , то примесное состояние сохраняет свою индивидуальность.
, то примесное состояние сохраняет свою индивидуальность. ,
, эВ (сотни градусов).
эВ (сотни градусов).
 , где сомножитель
, где сомножитель  очень сильно зависит от концентрации примесей Nd.
очень сильно зависит от концентрации примесей Nd.
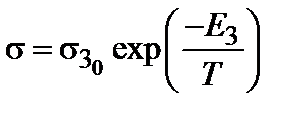 наличием термоактивационной зависимости проводимости.
наличием термоактивационной зависимости проводимости.  - сильная функция концентрации примесей.
- сильная функция концентрации примесей.
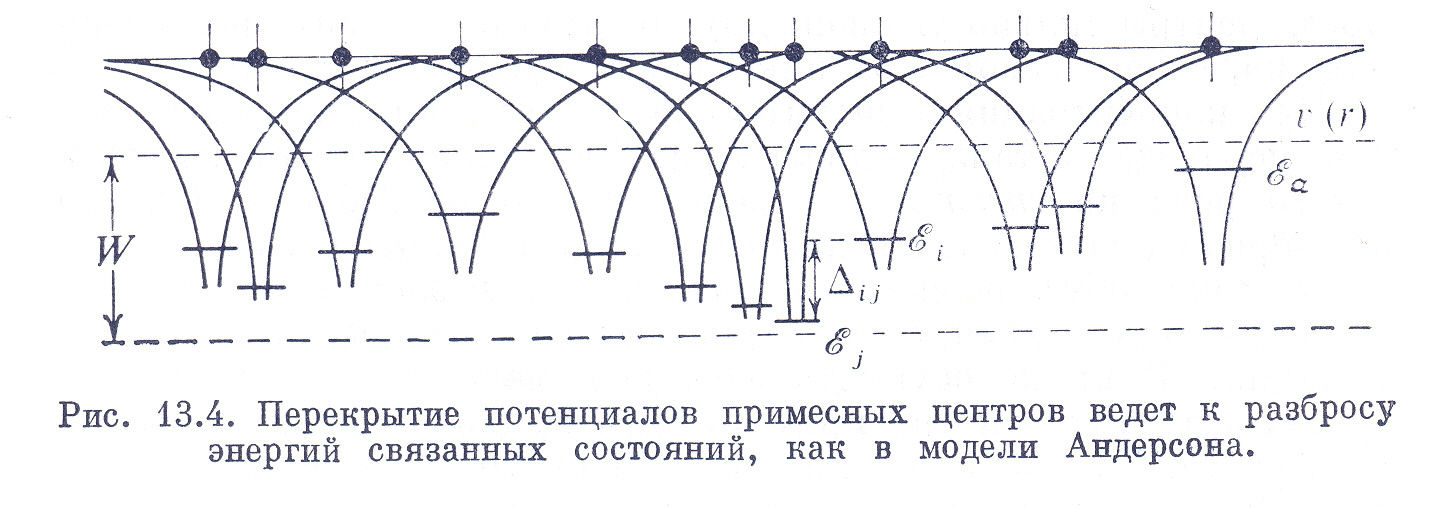 Рис. 8.4. Перекрытие потенциалов примесных центров ведет к разбросу энергий связанных состояний, как в модели Андерсона
Рис. 8.4. Перекрытие потенциалов примесных центров ведет к разбросу энергий связанных состояний, как в модели Андерсона




