Локализация электронов в неупорядоченных системах
Из эксперимента следует: - при малой концентрации примесей состояние электрона локализовано; - при большой концентрации примесей состояние электрона делокализовано; Можно предположить, что при определенных концентрациях примесей Будем рассматривать кристалл, в который введена примесь, создающая электронное состояние с энергией E 0 внутри запрещенной зоны. При увеличении концентрации Если примеси расположены регулярно, то можно использовать результаты решения, например, задачи Кронига-Пенни для любой концентрации примесей: - действительно, возникает размытие уровня в зону шириной W; - состояние, принадлежащее этой зоне, характеризуется волновым вектором Однако, качественно очевидно, что если Казалось бы, что причина локализации в хаотичном расположении примесей. Если примеси расположены хаотично то отсутствует трансляционная симметрия, следовательно Переход от локализации к делокализации, происходящей при изменении концентрации примесей (изменении энергии), называется переходом Андерсона. Учет сколь угодно слабых флуктуаций, рассматриваемый в одноэлектронном приближении, – переход Андерсена. Учет электрон-электронного взаимодействия в идеальных периодических системах – переход Мотта.
|

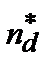 в примесной зоне появляется полоса энергий, для которой соответствующие состояния электронов – делокализованы, т.е. наличие трансляционной симметрии необязательно.
в примесной зоне появляется полоса энергий, для которой соответствующие состояния электронов – делокализованы, т.е. наличие трансляционной симметрии необязательно. плотность уровней с энергией порядка E 0 возрастает и при некоторой конечной концентрации
плотность уровней с энергией порядка E 0 возрастает и при некоторой конечной концентрации  и волновые функции близки к плоским волнам, т. е. делокализованы.
и волновые функции близки к плоским волнам, т. е. делокализованы.


