Простейшее предположение, которое можно сделать относительно фазовых переменных 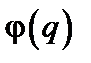 , состоит в их статистической независимости для различных величин q, изменяющихся в интервале
, состоит в их статистической независимости для различных величин q, изменяющихся в интервале 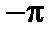 до
до  . Это предположение точно совпадает с концепцией спектрального беспорядка в решетке, использованной ранее для описания спиновых волн и фононов. Однако там речь шла о динамических модах, можно было предположить, что взаимодействие между ними невелико. В данном случае непрерывное случайное поле представляет собой статическую характеристику беспорядка, «замерзшего» в системе в процессе ее образования; представление о спектральном беспорядке здесь уже не обязательно. Более того, заметим, что фазовый угол
. Это предположение точно совпадает с концепцией спектрального беспорядка в решетке, использованной ранее для описания спиновых волн и фононов. Однако там речь шла о динамических модах, можно было предположить, что взаимодействие между ними невелико. В данном случае непрерывное случайное поле представляет собой статическую характеристику беспорядка, «замерзшего» в системе в процессе ее образования; представление о спектральном беспорядке здесь уже не обязательно. Более того, заметим, что фазовый угол 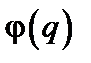 в действительности может выступать в роли измеряемой на опыте локальной характеристики поля. Действительно, эта величина зависит от объема образца и от некоторых незаданных граничных условий, определяющих квантование q в данном объеме. Искусственность упомянутого требования особенно подчеркивается тем обстоятельством, что фазовая переменная
в действительности может выступать в роли измеряемой на опыте локальной характеристики поля. Действительно, эта величина зависит от объема образца и от некоторых незаданных граничных условий, определяющих квантование q в данном объеме. Искусственность упомянутого требования особенно подчеркивается тем обстоятельством, что фазовая переменная 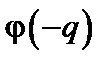 должна быть равна
должна быть равна 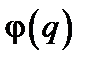 для каждого значения q, коль скоро мы требуем, чтобы функция
для каждого значения q, коль скоро мы требуем, чтобы функция  была вещественной.
была вещественной.
Преимущество этого метода реализуются в построении канонической формы случайного поля, статистические свойства которого определены для всех порядков функций распределения.
Действительно, распределение 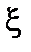 само по себе очень простое. Из выражений
само по себе очень простое. Из выражений
 ,
, 
в (произвольной) точке R = 0 мы получаем для вещественной величины 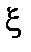 :
:
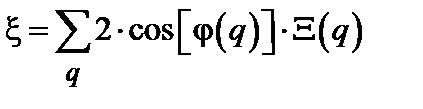 , (4.8)
, (4.8)
где фазы 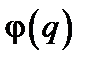 распределены случайно в интервале от
распределены случайно в интервале от 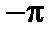 до
до  . Поскольку число членов этой суммы стремится к бесконечности, выражение (4.8) удовлетворяет условиям применимости центральной предельной теоремы теории вероятности.
. Поскольку число членов этой суммы стремится к бесконечности, выражение (4.8) удовлетворяет условиям применимости центральной предельной теоремы теории вероятности.
Указанное здесь условие необходимо, но еще недостаточно для того, чтобы была справедлива центральная предельная теорема. Нужно еще, чтобы дисперсия каждого слагаемого была ограниченной, а сумма этих дисперсий неограниченно возрастала при стремлении числа членов суммы к бесконечности.
В теории вероятностей показывается, что в этом случае переменная 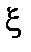 подчиняется стандартному нормальному или гауссову распределению:
подчиняется стандартному нормальному или гауссову распределению:
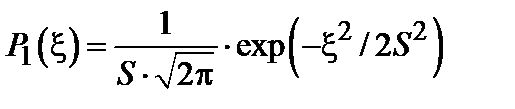 , (4.9)
, (4.9)
где 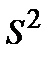 есть дисперсия случайного поля, т. е.
есть дисперсия случайного поля, т. е. 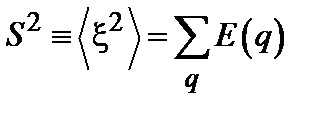 .
.
Таким образом, рассматриваемое случайное поле определяется величиной S и видом автокорреляционной функции 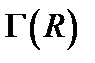 , в данном случае не приходится обращаться к спектральному представлению.
, в данном случае не приходится обращаться к спектральному представлению.
Многоточечные распределения и более высокие моменты случайного поля также можно явно вычислить с помощью стандартных методов теории вероятностей.
Так, например, двухточечное распределение должно быть, по сути дела, не чем иным, как совместным распределением Гаусса для переменных с корреляционной функцией 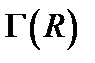 , т. e.
, т. e.
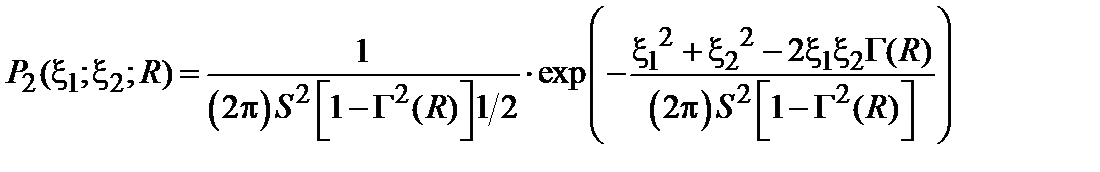 .(4.10)
.(4.10)
Из выражения (4.10) видно, что функция 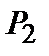 удовлетворяет условию
удовлетворяет условию
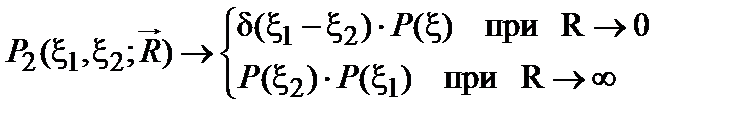 .
.
Поскольку многие физические свойства систем, обусловленные случайными полями, зависят от этой функции, то формула (4.10) оказывается очень полезной.
Однако условие спектрального беспорядка для гауссовой статистики очень искусственно. Возникает вопрос, при каких других общих условиях будут справедливы соотношения (4.9) и (4.10).
В соответствии с центральной предельной теоремой это возможно в случае, когда функцию  удается представить в виде суммы большого числа независимых случайных переменных.
удается представить в виде суммы большого числа независимых случайных переменных.
В качестве примера применения этого правила к стационарной случайной функции времени можно привести теорему Кэмпбелла. Дробовой шум тока в электрической цепи можно записать в виде суммы функций отклика 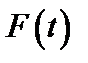 :
:
 , (4.11)
, (4.11)
где времена прихода электронов tj случайны и независимы. Теорема Кэмпбелла гласит, что распределение I (t) переходит в гауссово распределение, если скорость прихода электронов неограниченно возрастает.
Аналогично, в трехмерном случае поле должно быть представлено в виде суперпозиции «потенциалов», центрированных в случайных точках 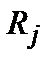 с объемной плотностью N, т. е.
с объемной плотностью N, т. е. 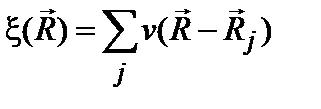 .
.
Из соотношения (4.1) следует условие: 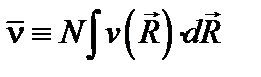 . Обобщая доказательство теоремы Кэмпбелла (или любой другой эквивалентный пример применения центральной предельной теоремы), мы можем убедиться, что при
. Обобщая доказательство теоремы Кэмпбелла (или любой другой эквивалентный пример применения центральной предельной теоремы), мы можем убедиться, что при  распределение x стремится к гауссову с дисперсией:
распределение x стремится к гауссову с дисперсией: 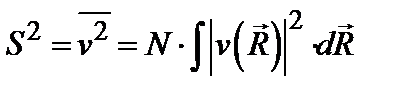 .
.
Разумеется, полученный результат имеет смысл, только если величина 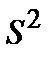 остается ограниченной в пределе при
остается ограниченной в пределе при  . Физически этот предел недостижим, но в ряде случаев обращение к нему дает вполне реалистичную аппроксимацию.
. Физически этот предел недостижим, но в ряде случаев обращение к нему дает вполне реалистичную аппроксимацию.
В суперпозиционном приближении корреляционная функция оказывается просто автокорреляционной функцией потенциала 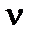 , нормированной на единицу:
, нормированной на единицу:
 .
.
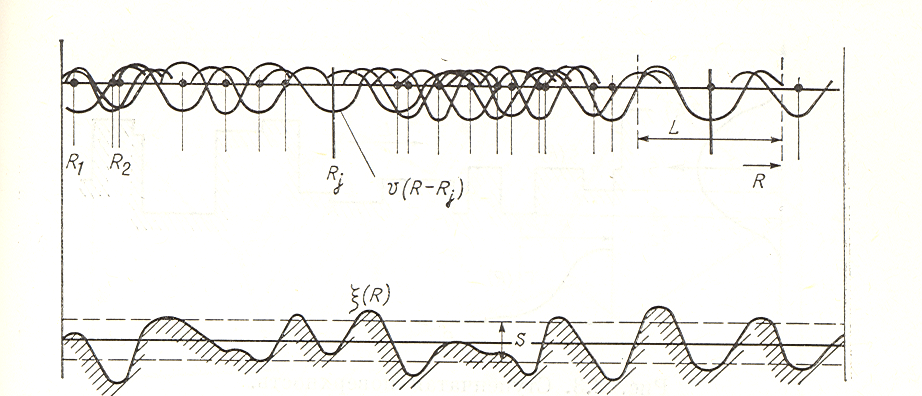
Рис. 4.2.. Суперпозиция случайно разбросанных потенциалов, создающих гауссов беспорядок.
Возникает вопрос: при каких условиях гауссов предел дает хорошую аппроксимацию?
Основное условие применимости этого приближения состоит в том, чтобы величина 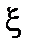 в каждой точке поля представляла собой сумму достаточно большого числа независимых слагаемых.
в каждой точке поля представляла собой сумму достаточно большого числа независимых слагаемых.
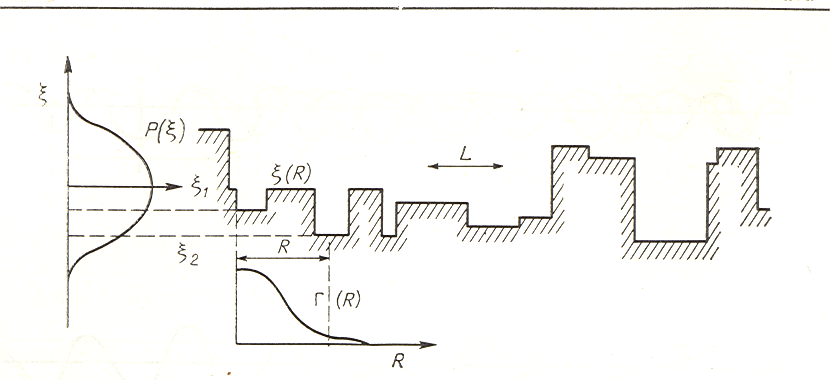 Чтобы понять, как может возникнуть негауссово поле, рассмотрим ступенчатую поверхность
Чтобы понять, как может возникнуть негауссово поле, рассмотрим ступенчатую поверхность
Рис. 4.3. Ступенчатая поверхность.
Двухточечной функцией этого распределения:

Эта функция удовлетворяет всем условиям, независимо от вида 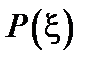 или
или  , однако, даже если функция
, однако, даже если функция 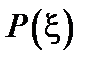 намеренно выбирается в гауссовом виде, то и тогда двухточечная функция распределения не совпадает с совместным гауссовым распределением (4). Говоря топографическим языком, рассматриваемая поверхность состоит из набора горизонтальных плато, разделенных резкими уступами, причем расстояния между плато по порядку величины равны корреляционной длине L. По аналогии с телеграфной функцией, удобно предположить, что корреляционная и спектральной плотности функции в данном случае имеют соответственно вид:
намеренно выбирается в гауссовом виде, то и тогда двухточечная функция распределения не совпадает с совместным гауссовым распределением (4). Говоря топографическим языком, рассматриваемая поверхность состоит из набора горизонтальных плато, разделенных резкими уступами, причем расстояния между плато по порядку величины равны корреляционной длине L. По аналогии с телеграфной функцией, удобно предположить, что корреляционная и спектральной плотности функции в данном случае имеют соответственно вид:
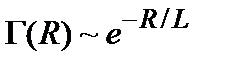 ;
; 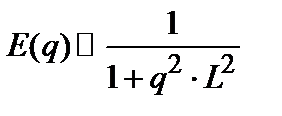 ,
,
как будто интервалы между ступеньками распределены случайным образом. Однако только этого предположения недостаточно для адекватного определения топологии «скачков» между соседними плато, вследствие чего модель нуждается в дальнейшем аналитическом исследовании.
Из-за разрывов в функции  здесь возникает слишком много коротковолновых компонент. Ответ заключается в том, что фазы
здесь возникает слишком много коротковолновых компонент. Ответ заключается в том, что фазы 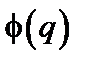 оказываются коррелированными, связь между ними должна обеспечивать горизонтальность поверхностей ступенек. Эти ограничения бесконечно сложны, и их никогда не удается выразить в явном виде, вместе с тем о них нельзя забывать при статистическом описании поля.
оказываются коррелированными, связь между ними должна обеспечивать горизонтальность поверхностей ступенек. Эти ограничения бесконечно сложны, и их никогда не удается выразить в явном виде, вместе с тем о них нельзя забывать при статистическом описании поля.

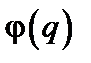 , состоит в их статистической независимости для различных величин q, изменяющихся в интервале
, состоит в их статистической независимости для различных величин q, изменяющихся в интервале 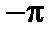 до
до  . Это предположение точно совпадает с концепцией спектрального беспорядка в решетке, использованной ранее для описания спиновых волн и фононов. Однако там речь шла о динамических модах, можно было предположить, что взаимодействие между ними невелико. В данном случае непрерывное случайное поле представляет собой статическую характеристику беспорядка, «замерзшего» в системе в процессе ее образования; представление о спектральном беспорядке здесь уже не обязательно. Более того, заметим, что фазовый угол
. Это предположение точно совпадает с концепцией спектрального беспорядка в решетке, использованной ранее для описания спиновых волн и фононов. Однако там речь шла о динамических модах, можно было предположить, что взаимодействие между ними невелико. В данном случае непрерывное случайное поле представляет собой статическую характеристику беспорядка, «замерзшего» в системе в процессе ее образования; представление о спектральном беспорядке здесь уже не обязательно. Более того, заметим, что фазовый угол 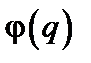 в действительности может выступать в роли измеряемой на опыте локальной характеристики поля. Действительно, эта величина зависит от объема образца и от некоторых незаданных граничных условий, определяющих квантование q в данном объеме. Искусственность упомянутого требования особенно подчеркивается тем обстоятельством, что фазовая переменная
в действительности может выступать в роли измеряемой на опыте локальной характеристики поля. Действительно, эта величина зависит от объема образца и от некоторых незаданных граничных условий, определяющих квантование q в данном объеме. Искусственность упомянутого требования особенно подчеркивается тем обстоятельством, что фазовая переменная 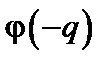 должна быть равна
должна быть равна 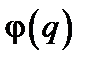 для каждого значения q, коль скоро мы требуем, чтобы функция
для каждого значения q, коль скоро мы требуем, чтобы функция  была вещественной.
была вещественной.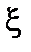 само по себе очень простое. Из выражений
само по себе очень простое. Из выражений ,
, 
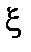 :
: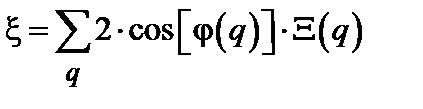 , (4.8)
, (4.8)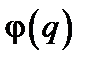 распределены случайно в интервале от
распределены случайно в интервале от 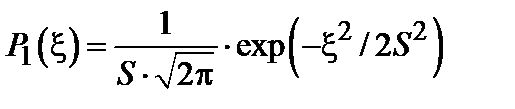 , (4.9)
, (4.9)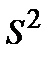 есть дисперсия случайного поля, т. е.
есть дисперсия случайного поля, т. е. 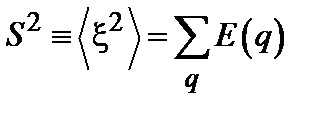 .
.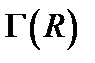 , в данном случае не приходится обращаться к спектральному представлению.
, в данном случае не приходится обращаться к спектральному представлению.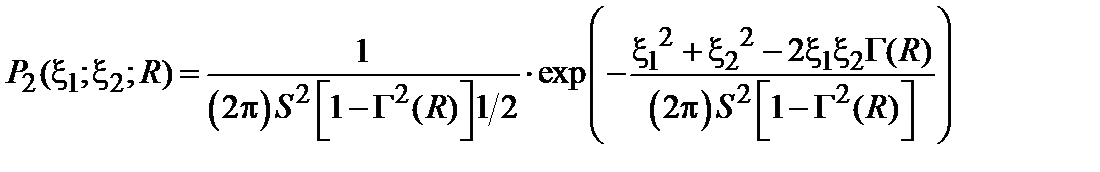 .(4.10)
.(4.10)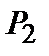 удовлетворяет условию
удовлетворяет условию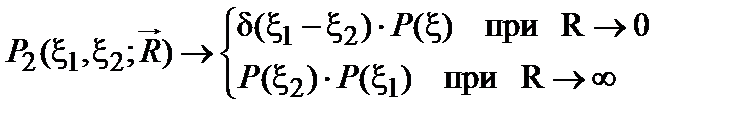 .
.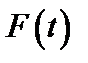 :
: , (4.11)
, (4.11)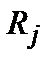 с объемной плотностью N, т. е.
с объемной плотностью N, т. е. 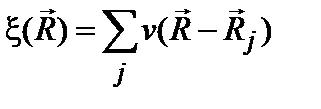 .
.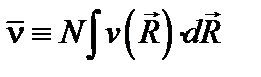 . Обобщая доказательство теоремы Кэмпбелла (или любой другой эквивалентный пример применения центральной предельной теоремы), мы можем убедиться, что при
. Обобщая доказательство теоремы Кэмпбелла (или любой другой эквивалентный пример применения центральной предельной теоремы), мы можем убедиться, что при  распределение x стремится к гауссову с дисперсией:
распределение x стремится к гауссову с дисперсией: 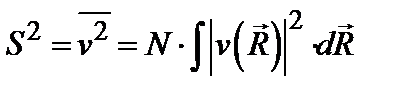 .
.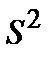 остается ограниченной в пределе при
остается ограниченной в пределе при 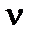 , нормированной на единицу:
, нормированной на единицу: .
.
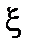 в каждой точке поля представляла собой сумму достаточно большого числа независимых слагаемых.
в каждой точке поля представляла собой сумму достаточно большого числа независимых слагаемых. Чтобы понять, как может возникнуть негауссово поле, рассмотрим ступенчатую поверхность
Чтобы понять, как может возникнуть негауссово поле, рассмотрим ступенчатую поверхность
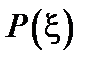 или
или  , однако, даже если функция
, однако, даже если функция 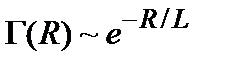 ;
; 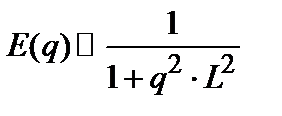 ,
, здесь возникает слишком много коротковолновых компонент. Ответ заключается в том, что фазы
здесь возникает слишком много коротковолновых компонент. Ответ заключается в том, что фазы 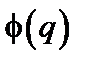 оказываются коррелированными, связь между ними должна обеспечивать горизонтальность поверхностей ступенек. Эти ограничения бесконечно сложны, и их никогда не удается выразить в явном виде, вместе с тем о них нельзя забывать при статистическом описании поля.
оказываются коррелированными, связь между ними должна обеспечивать горизонтальность поверхностей ступенек. Эти ограничения бесконечно сложны, и их никогда не удается выразить в явном виде, вместе с тем о них нельзя забывать при статистическом описании поля.


