Жидкие кристаллы, состоящие из несферических молекул

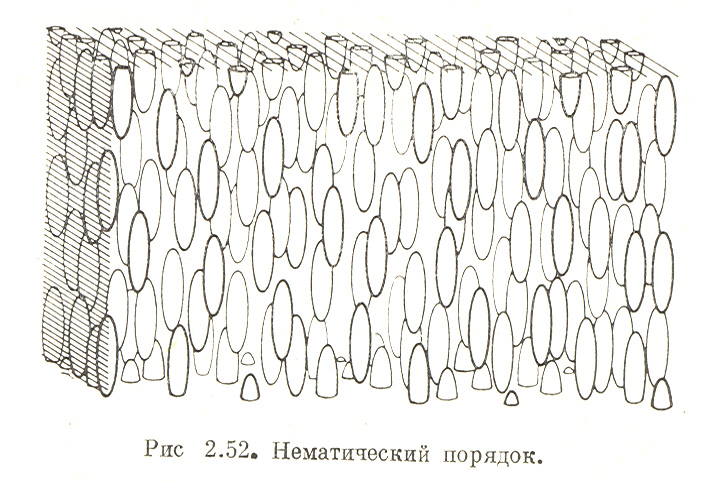
Форма молекул жидкости должна заметно влиять на их структурное расположение. Однако статистические теории жидкого состояния почти всегда имеют дело с приблизительно сферическими молекулами, взаимодействующими посредством центральных сил. Пожалуй, исключая расчеты структуры воды по методу молекулярной динамики, вряд ли можно найти надежные теоретические результаты для жидкостей, состоящих из несферических молекул. Тот факт, что вблизи точки плавления плотность упаковки для большинства молекулярных жидкостей по порядку величины составляет 0, 5 – 0, 6, означает, что пространство довольно сильно заполнено. Однако это мало что говорит о статистических характеристиках системы. Теория термодинамических свойств жидкости до сих пор носит, в сущности, феноменологический характер и не вносит ничего существенного в математическую теорию беспорядка.

Введем упрощающее предположение, состоящее в том, что каждая молекула считается идеально твердой и аксиально симметричной, наподобие эллипсоида или гантели. Для статистического описания жидкости, состоящей из таких молекул, надо знать функции распределения относительных ориентации осей двух или большего числа молекул в любой данной пространственной конфигурации. Ясно, что это гораздо более сложная геометрическая задача, чем расчет радиальной функции распределения g (В) для сферических атомов.

Из опыта известно, что очень длинные твердые молекулы не могут упаковываться вместе без того, чтобы не возникли корреляции в их относительных ориентациях. Именно таково происхождение многочисленных захватывающих эффектов, наблюдаемых в жидких кристаллах. Так, например, в нематической жидкости (рис.3.16) центры молекул не образуют регулярную решетку, однако существует дальний порядок в ориентации их продольных осей.

Рис. 3.16. Нематический порядок в жидких кристаллах