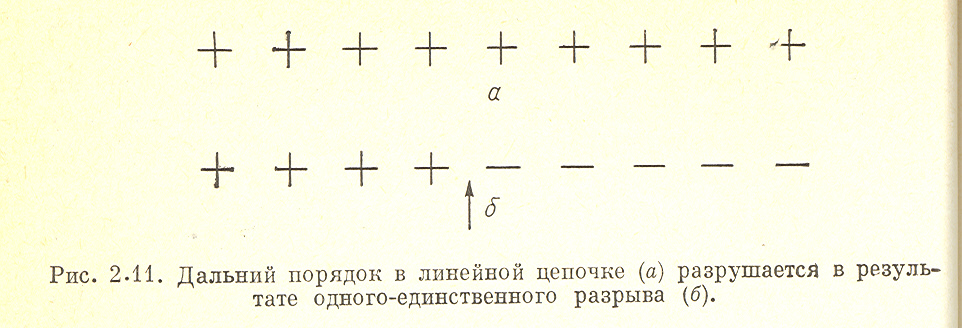Размерность и порядокКак известно, одномерная решетка будет термически неустойчива. В самом деле, принимая во внимание довольно общие условия, которым удовлетворяет радиус действия межатомных сил, можно показать, что в одно- или двумерных системах спонтанный кристаллический порядок существовать не может. Воспользуемся моделью гармонических колебаний решетки и произведем обычные Фурье преобразования к фононным переменным. Тогда кроме формулы для корреляционной функции (см. лекцию) можно получить еще следующее соотношение:
Нас интересует поведение суммы в правой части этого соотношения при больших значениях R. Знаменатель можно заменить на
При d = 1 этот интеграл пропорционален R; при d = 2 он ведет себя асимптотически как ln R. В обоих случаях флуктуации расстояния между атомами в удаленных друг от друга узлах неограниченно возрастают по мере увеличения этого расстояния. С другой стороны, при d = 3 интеграл сходится к малой величине, не зависящей от R, так что предполагаемый порядок в решетке оказывается стабильным. Очень сходный с этим результат легко получить для спиновой корреляционной функции В одномерной модели Изинга состояние спонтанного упорядочения термодинамически неустойчиво (рис.3.2).
Рис. 3.2. Дальний порядок в линейной цепочке (а) разрушается в результате одного единственного разрыва (б).
|
.
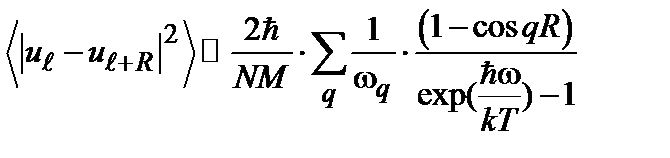и положить (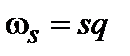
, где s - скорость звука). Интересуясь d -мерной решеткой, получим:
.
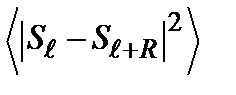, где R - расстояние между удаленными узлами в упорядоченной ферромагнитной цепочке. Таким образом, в одно- или двумерной системе в отсутствие факторов, изменяющих спектр магнонов (конечного магнитного поля или магнитной анизотропии), спонтанный ферромагнитный или антиферромагнитный порядок возникнуть не может.
