Спектральный беспорядок
Пусть произвольная случайная переменная
Рассмотрим статистическую корреляционную функцию:
Корреляционная функция представляет собой фурье-образ квадрата спектральной амплитуды возбуждения. (Эта теорема оказывается верной и в общем случае). При соответствующих условиях спектральное представление беспорядка заметно упрощает задачу. Введем дополнительную гипотезу: пусть амплитуды мод Рассмотрим модель спектрального беспорядка на примере задачи о спиновых волнах в ферромагнетике. Будем исходить из системы с гамильтонианом:
предполагая, что она близка к идеально упорядоченному состоянию, когда параметр дальнего порядка близок к единице. Переменная Продольная спиновая корреляционная функция задается выражением:
С помощью стандартных линейных преобразований можно привести гамильтониан к виду:
Пусть обменное взаимодействие распространяется только на z ближайших соседей, находящихся на расстоянии a. Далее, запишем выражение для спектра магнонов:
Поскольку в последующих выкладках будем работать в области малых q, то можем разложить экспоненту по аргументу и раскрыть сумму по взаимно противоположным соседям:
Средний квадрат амплитуды или, что то же самое, магнонное число заполнения выражается через обычную функцию распределения:
В приближении
Рассмотрим корреляционную функцию при больших R. Сумму теперь можно заменить интегралом. Учитывая, что основной вклад дадут слагаемые с малым q, получим:
В последнем интеграле, переходя к сферическим координатам, запишем:
пропорциональна При
|

 соответствует узлу решетки с номером
соответствует узлу решетки с номером  . Роль этой переменной может играть, например, магнитный момент локализованного спина или смещение атома из своего узла. Предположим, что рассматриваемая физическая модель обладает трансляционной инвариантностью решетки. Тогда возможно ввести новые переменные с помощью преобразования Фурье:
. Роль этой переменной может играть, например, магнитный момент локализованного спина или смещение атома из своего узла. Предположим, что рассматриваемая физическая модель обладает трансляционной инвариантностью решетки. Тогда возможно ввести новые переменные с помощью преобразования Фурье: ,
,  .
. . Для нее можно получить:
. Для нее можно получить: .
.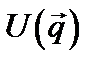 статистически независимы для разных
статистически независимы для разных  . Такую систему можно рассматривать как спектрально неупорядоченную. Действительно, статистические свойства ее определяются скорее переменными в обратном пространстве, а не в пространстве узлов.
. Такую систему можно рассматривать как спектрально неупорядоченную. Действительно, статистические свойства ее определяются скорее переменными в обратном пространстве, а не в пространстве узлов. ,
, будет обозначать амплитуду отклонения спина от максимального значения
будет обозначать амплитуду отклонения спина от максимального значения  . Введем операторы рождения и уничтожения спиновой волны –
. Введем операторы рождения и уничтожения спиновой волны –  ,
,  .
. .
.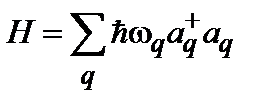 ,
,

 .
. получим
получим .
. , (2.20) где
, (2.20) где  .
. Таким образом, продольная спиновая корреляционная функция
Таким образом, продольная спиновая корреляционная функция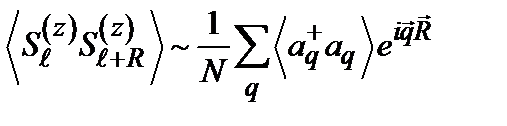
 , причем характерная длина ее изменения (длина корреляции)
, причем характерная длина ее изменения (длина корреляции) 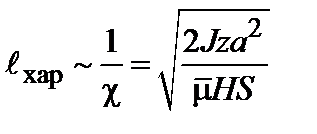 . (2.21)
. (2.21) ,
,  .Видно, что, поскольку
.Видно, что, поскольку  , то чем больше взаимодействие между спинами, тем дальше в системе распространяется корреляция.
, то чем больше взаимодействие между спинами, тем дальше в системе распространяется корреляция.


