Магнетики
Ближний порядок возникает за счет короткодействующих сил взаимодействия между атомами или спинами. Например, в случае магнетика вводится гамильтониан Гейзенберга, состоящий из суммы слагаемых вида Они описывают взаимодействие между спинами, расположенными в узлах
Рис. 2.11. а – конфигурация частиц в модели Изинга. Она может описывать: б – расположение спинов; в – расположение атомов в бинарном сплаве; г – расположение частиц в решеточном газе.
В общем случае обменный интеграл
Гамильтониан модели Изинга получается отсюда, если наложить на спины условие квантования
Сплавы Модель Изинга можно использовать для описания межатомных взаимодействий в бинарном сплаве. Допустим, например, что парам атомов АА, АВ и ВВ отвечают соответственно энергии
При этом числа пар каждого типа ограничены соотношениями
Далее, по условию, число sравно +1 или -1 в зависимости от того, занят ли данный узел атомом типа А или B. Отсюда вытекает дальнейшее соотношение:
Соответственно для энергии получаем:
С точностью до постоянного слагаемого это выражение совпадает с правой частью формулы (2.10). Таким образом, ближний порядок в сплаве будет таким же, как и в магнетике Изинга, если роль «обменного интеграла» и напряженности магнитного поля играют соответственно выражения
Так, например, если J > 0, то атомы данного сорта стремятся объединиться в кластеры, подобно тому, как в ферромагнетике предпочтительной оказывается параллельная ориентация спинов. С другой стороны, при J < 0 наблюдается тенденция к образованию пар неодинаковых атомов - соответственно противоположным спинам в антиферромагнетике. Однако, если энергия, необходимая для замещения атома А атомом В, не зависит от состояния ближайших соседей и величина J обращается в нуль, то система оказывается совершенно неупорядоченной. В случае «решеточного газа» выражение для энергии дается по-прежнему формулой (2.11), только под
|

 .
. и
и  . По условию при обменном интеграле
. По условию при обменном интеграле  стоит знак минус, так что случаю ферромагнитного упорядочения (т. е. параллельным спинам) соответствует положительное значение J. В полный гамильтониан системы вводится и слагаемое, описывающее влияние внешнего магнитного поля на магнитный момент каждого спина
стоит знак минус, так что случаю ферромагнитного упорядочения (т. е. параллельным спинам) соответствует положительное значение J. В полный гамильтониан системы вводится и слагаемое, описывающее влияние внешнего магнитного поля на магнитный момент каждого спина . (2.8)
. (2.8)
 . Однако, практически чаще всего имеют дело с моделями, в которых этот интеграл считается отличным от нуля только для ближайших или ближайших и следующих за ними соседей. Для некоторых особых типов кристаллов можно ввести анизотропное взаимодействие, рассматривая J как тензор. При этом
. Однако, практически чаще всего имеют дело с моделями, в которых этот интеграл считается отличным от нуля только для ближайших или ближайших и следующих за ними соседей. Для некоторых особых типов кристаллов можно ввести анизотропное взаимодействие, рассматривая J как тензор. При этом . (2.9)
. (2.9) и пренебречь величиной
и пренебречь величиной  . Переобозначив соответствующие переменные, получим
. Переобозначив соответствующие переменные, получим (2.10)
(2.10)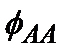 ,
,  ,
, 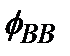 . Тогда полная энергия системы запишется в виде
. Тогда полная энергия системы запишется в виде
 и
и  .
.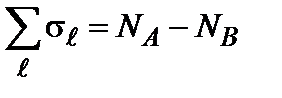 ,
, 
 (2.11)
(2.11)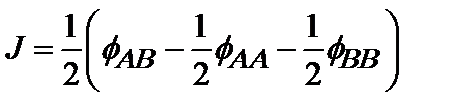 ,
,  .
. =
=  = 0 обозначает энергии, связанные с наличием «дырок».
= 0 обозначает энергии, связанные с наличием «дырок».


