Эргодическая теорема. Физически достоверный объем
В макроскопическом опыте мы имеем дело с полным объемом образца или с его большой макроскопической частью. Таким образом, все наблюдаемые в эксперименте величины получались в результате усреднения по объему образца. Макроскопически большой образец можно представить как совокупность большого числа макроскопических подобластей. Физически ясно, что значения потенциальной энергии электронов в случайном поле, в окрестностях точек, значительно удаленных друг от друга, не будут связаны между собой (между ними не будет корреляционной связи). Действительно, при значительном удалении, в каждом подобразце будет наблюдаться своя случайная реализация случайного поля, т.е. свое расположение примесей. Усреднение по объему сведется к усреднению по различным реализациям случайного поля, т.е. по всем возможным конфигурациям атомов примесей. Такая процедура усреднения не имеет аналогов в обычной (зонной) теории идеального кристалла. Усреднение по объему образца эквивалентно усреднению по функционалу вероятности Поскольку потенциальная энергия - случайная величина, то задача об энергетическом спектре частицы в случайном поле должна иметь вероятностный характер. Нет смысла спрашивать дозволено или нет то или иное значение энергии, принадлежит оно дискретному или непрерывному спектру. Ответ должен носить вероятностный характер. Можно говорить об энергетическом спектре только с точки зрения теории вероятностей. Обязательным является предельный переход
Предположим, что прошлись по малому образцу: Встретились только 3 конфигурации дефектов (случайного поля) (рис.1.7).
Рис.1.7. Качественная картина к определению физически достоверного объема образца.
Если рассмотреть больший образец, то там может встретиться больше конфигураций. Физически достоверный объем – объем, в котором вероятность встретить все возможные конфигурации соответствует представительности конфигураций в бесконечном объеме. Краткие выводы: В силу отсутствия дальнего порядка, квазиимпульс, характеризующий состояние системы, не является хорошим квантовым числом. Такое состояние с каким-либо значением k - нестационарное, оно разрушается. Рассеяние заряда на непериодическом поле столь интенсивно, что квазиимпульс не сохраняется даже приближенно: - закон дисперсии - энергия Ферми eF не определяется. В ФТТ все измеряемые величины определяются их значением на уровне Ферми; - эффективная масса носителей - понятие зоны Бриллюэна отсутствует; - в основе физики идеального твердого тела лежит одноэлектронное приближение. Задача сводится к квазичастицам, динамической характеристикой которых становится эффективная масса (электрона, дырки). В идеальном кристалле инкремент затухания одноэлектронного представления стремится к нулю вблизи поверхности Ферми, что обусловлено совместным выполнением принципа Паули, законами сохранения энергии и квазиимульса. Когда поле непериодично, то инкремент затухания одноэлектронного представления оказывается ненулевым. Таким образом, в непериодических системах, по сравнению с идеальными кристаллом, возрастает роль многочастичных эффектов. В неидеальном кристалле (непериодическом) – необходимо решать многочастичную задачу. Утверждение: Для любой системы, как угодно взаимодействующих частиц, можно ввести понятие плотности числа состояний, и дать рецепт ее вычисления. Если плотность числа состояний известна, то все термодинамические величины могут быть вычислены и в общем случае. Как известно, для электронов (фермионы) вероятность заселения состояний с энергией E определяется распределением Ферми:
Функция плотности числа состояний дает информацию о том, существует ли такое состояние в системе, т.е. представлено ли это состояние. Напомним, вывод формулы для плотности электронного газа
здесь сумма по s есть суммирование по спиновым состояниям. Переход от интегрирования по импульсному пространству к интегрированию по энергии:
проводится с Якобианом перехода
В случае газа свободных квазичастиц (электронов) закон дисперсии:
а для плотности числа состояний
где Вся конкретная информация, необходимая для вычисления термодинамических величин, содержится в r(E). Этот результат может быть обобщен на случай наличия в системе локальных уровней. Пусть
Обобщая на случай кратности вырождения заполненных и пустых состояний - g 1, g 0, получим
Учитывая, что
Если ввести энергию
Тогда, плотность числа электронов
учитывает наличие не только непрерывного спектра, но дискретных уровней. Полная энергия электронов равна
Это термодинамические величины. Как известно, система также характеризуется кинетическими величинами, определяющими отклик системы на внешнее воздействие, например, проводимостью. В теории идеального твердого тела существует три теоремы о связи плотности числа состояний r(Е) и отклика системы на внешнее воздействие. Напомним основные моменты, определяющие проводимость системы для твердого тела. Если имеется электрическое поле, то расселение электронов по энергии меняется. Меняется и функция распределения: из равновесной
Плотность тока определяется соотношением
Используя этот подход для кристаллического твердого тела можно показать
Из этого следует, что кинетический коэффициент s также определяется плотностью числа состояния Пусть Отметим следующее: 1. Если электроны и дырки в равновесных условиях занимают дискретные уровни в запрещенной зоне, то они могут участвовать в переносе заряда только путем перескока по уровням или за счет заброса с уровня примеси в зону проводимости или валентную (для дырок); 2. Вероятность таких перескоков падает, при Т ® 0. 3. Если Т ® 0 и проводимость остается Существуют доказательства трех теорем о корреляциях для кристаллического твердого тела: Теорема 1. Проводимость не равна нулю при Т = 0, если уровень Ферми принадлежит области, где Теорема 2. Если уровень Ферми попадает в область, где r = 0, то при достаточно низких температурах проводимость
где Теорема 3. (о поглощении электромагнитного излучения) Коэффициент поглощения κ электромагнитного излучения с частотой w не равен нулю, если частота электромагнитного излучения соответствует условию:
где Можно сделать следующее обобщение на случай некристаллического твердого тела. В любой системе как угодно взаимодействующих частиц можно ввести понятие плотности числа состояний и дать рецепт ее вычисления. При этом связь системы с термодинамическими величинами сохранится. Теоремы 1, 2, 3 о корреляциях остаются применимыми. Подводя итог, можно сказать следующее. Запрещенной зоной называется область энергий, где
|

 .
.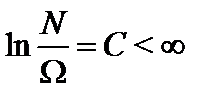 ,
, ,
,  - объем и число частиц в этом объеме, константа С не является функцией объема.
- объем и число частиц в этом объеме, константа С не является функцией объема.
 - теряет смысл;
- теряет смысл; теряет смысл;
теряет смысл; . (1.8)
. (1.8) ,
,

 , где
, где  - плотность состояний.
- плотность состояний.
 ,
, , (1.9)
, (1.9)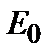 – дно зоны проводимости, от которого проводится отсчет энергии E.
– дно зоны проводимости, от которого проводится отсчет энергии E. – общее число примесей в состоянии с энергией
– общее число примесей в состоянии с энергией 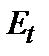 ,
,  – число заселенных состояний,
– число заселенных состояний,  – число пустых состояний. Тогда
– число пустых состояний. Тогда . (1.10)
. (1.10) ,
, 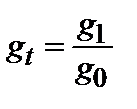 .
. , получим
, получим . (1.11)
. (1.11) , то можно обобщить плотность числа состояний на локализованные
, то можно обобщить плотность числа состояний на локализованные .
. ,
,  (1.12)
(1.12) . (1.13)
. (1.13) она становится неравновесной g (E):
она становится неравновесной g (E): .
.
 .
. . (1.14)
. (1.14) .
. в области непрерывного спектра, имеет особенности в точках дискретного спектра и обращается в нуль в точках запрещенных значений энергии.
в области непрерывного спектра, имеет особенности в точках дискретного спектра и обращается в нуль в точках запрещенных значений энергии.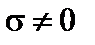 , то в зоне проводимости остается конечное число носителей.
, то в зоне проводимости остается конечное число носителей. и непрерывна.
и непрерывна. ,
, – ближайшая к уровню Ферми F граница области спектра, для которой
– ближайшая к уровню Ферми F граница области спектра, для которой  ,
, ,
, 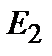 – значения энергий, для которых
– значения энергий, для которых  ,
,  (непрерывность r необязательна).
(непрерывность r необязательна).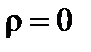 или
или  -образные особенности. Этим точкам отвечают дискретные уровни (т.е. локализованные состояния электрона). Термин " запрещенная зона" меняется на более общее понятие - " щель для подвижности". Для описания беспорядка в системе вводят различные модели беспорядка. Модели вводятся с некоторыми предположения о вероятности тех или иных событий.
-образные особенности. Этим точкам отвечают дискретные уровни (т.е. локализованные состояния электрона). Термин " запрещенная зона" меняется на более общее понятие - " щель для подвижности". Для описания беспорядка в системе вводят различные модели беспорядка. Модели вводятся с некоторыми предположения о вероятности тех или иных событий.


