ВВЕДЕНИЕ. Отрывок из произведения Д.С.Лихачева посвящен встрече человека с русской культурой

Отрывок из произведения Д.С.Лихачева посвящен встрече человека с русской культурой. Автор хочет, чтобы у каждого сложилось свое, собственное отношение и к памятникам архитектуры, и к истории страны, и к природе. Умение «ценить свое» в увиденном – это способ стать личностью, а не частью толпы.

В этом произведении Д.С.Лихачев описывает свой родной город – Петербург. Этот прекрасный город описывали столько раз! Все знают, что в нем есть знаменитые достопримечательности: центр Невы и Петропавловская крепость, в которой в полдень стреляет пушка. А автор говорит о том, что любит совсем другие места – каналы. Они вносят «оживление и беспорядок в казенную бездушную геометрию улиц». Здесь он вспоминает сюжет романа Достоевского.

Каждый город «наводит на размышления», потому что у него есть свое лицо. Я думаю, что наша родина может гордиться любым своим уголком: в Томске и Вологде есть деревянная резьба, в Костроме и Ярославле – набережные и бульвары. Я хочу согласиться с Д.С.Лихачевым, он совершенно прав: нет на земле неинтересных мест. А еще он говорит нам, что надо воспитывать умение видеть интересное, нельзя поддаваться скуке.

В этом тексте автор использует разные средства языковой выразительности: это метафоры (город «проплывает» мимо реки, канал «размыл» планировку), ряды однородных членов, интересные эпитеты («торжественный ход льда», «ужасная легенда»). Отрывок построен так, что от собственных впечатлений о тоскливой Петропавловской крепости и «приватных местах» своего родного города Д.С.Лихачев перешел к рассуждениям, как строили в Древней Руси, от которой пошли три современных государства. Но мне больше всего понравилось, как связаны в этом тексте русские города и русские книги. Ведь герои Тургенева, Островского, Горького, Гончарова, которых мы знаем иногда с детства, ходили тем по улицам, где можешь пройти и ты!

Мне кажется, что для Д.С.Лихачева культура – это главный способ понимания себя и своей страны.

 

 

ОГЛАВЛЕНИЕ

 

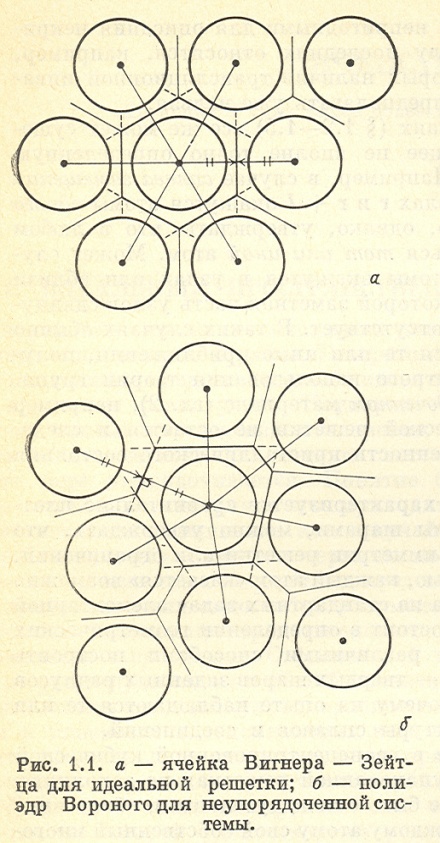
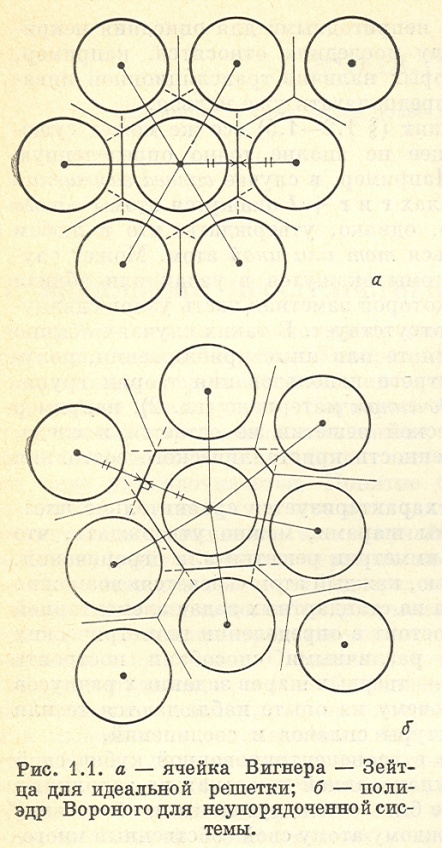
Введение.................................................................................. 3

РАЗДЕЛ 1. Неупорядоченная конденсированная система с высокой концентрацией дефектов 8

1.1. Основные примеры неупорядоченных конденсированных систем 13

1.2. Некоторые экспериментальные данные по неупорядоченным системам 16

1.3. Эргодическая теорема. Физически достоверный объем 22

РАЗДЕЛ 2. Модели и метрика ячеистого беспорядка....... 29

2.1. Беспорядок замещения..................................................... 29

2.2. Магнитный беспорядок..................................................... 31

2.3. «Ледовый» беспорядок..................................................... 38

2.4. Метрика ячеистого беспорядка........................................ 41

2.5. Применение модели Изинга для различных неупорядоченных систем ячеистого беспорядка 43

2.5.1. Магнетики....................................................................... 43

2.5.2. Сплавы............................................................................ 45

2.5.3. Сегнетоэлектрики........................................................... 46

2.6. Дальний порядок............................................................... 46

2.7. Размер и области упорядочения и упорядоченные домены 50

2.8. Спектральный беспорядок................................................ 55

2.9. Термодинамика ячеистого беспорядка............................ 59

2.10. Ближний порядок и корреляции..................................... 60

2.11. Подобие и группа перенормировки в теории критических явлений 65

РАЗДЕЛ 3. Модели и метрика топологического беспорядка 67

3.1. Беспорядок на уровне атомной структуры............ 67

3.2. Размерность и порядок

3.3. Неупорядоченные линейные цепочки.............................. 71

3.3.1. Модель Кронига – Пенни для неупорядоченной цепочки 73

3.4. Приводимый и неприводимый топологический беспорядок 74

3.5. Физическая реализация одномерных систем.................. 75

3.6. Дислокационный беспорядок.......................................... 78

3.7. Поликристаллический беспорядок.................................. 79

3.7.1. Атомные функции распределения................................ 80

3.7.2. Аморфный или паракристаллический?........................ 85

3.8. Жидкие кристаллы, состоящие из несферических молекул 87

3.9. Беспорядок газового типа................................................. 88

РАЗДЕЛ 4. Модели и метрика континуального беспорядка 90

4.1. Континуальные модели.................................................... 90

4.2. Однородные случайные поля........................................... 92

4.3. Гауссовы случайные поля................................................ 96

РАЗДЕЛ 5. Наблюдение беспорядка.................................... 102

РАЗДЕЛ 6. Возбуждения в неупорядоченных системах... 109

6.1 Возбуждения в неупорядоченных системах.................... 109

6.2. Возбуждения в одномерных системах............................ 114

6.2. Фазовое представление.................................................... 118

6.3. Запрещенные зоны в спектрах неупорядоченных цепочек 122

6.4. Плотность состояний........................................................ 126

6.5. Приближение локальной плотности................................ 128

6.6. Квазиклассические электроны в случайном потенциальном рельефе 133

РАЗДЕЛ 7. Перколяция......................................................... 140

7.1 Введение. Терминология................................................... 140

7.2. Задачи перколяции на регулярных решетках.................. 143

7.3. Перколяция на решетка Бёте............................................ 147

7.4. Регулярные решетки: плоские и пространственные....... 150

7.5. Порог протекания для объемных решеток...................... 153

7.6 Оценка порога протекания задачи узлов.......................... 156

7.7. Задача координационных сфер........................................ 160

7.8. Структура бесконечного кластера. Модель Шкловского –Де Жена. 164

7.9. Роль размеров системы.................................................... 168

7.10. Электропроводность вблизи порога протекания.......... 171

7.11. Мощность скелета бесконечного кластера вблизи порога протекания. Роль мертвых концов.................................................................................................. 174

РАЗДЕЛ 8. Теория прыжковой проводимости.................. 175

8.1. Прыжковая проводимость................................................ 181

8.2. Концентрационная зависимость прыжковой проводимости 186

8.3. Температурная зависимость прыжковой проводимости 187

РАЗДЕЛ 9. Локализация и делокализация носителей. Анализ с точки зрения перколяционного подхода.................................................................................... 190

9.1. Локализация электронов в неупорядоченных системах. 190

9.2. Узкие зоны и переход Мотта............................................ 192

9.3. Модель Андерсона............................................................ 197

9.4. Связь плотности числа состояний с критерием локализации 199

РАЗДЕЛ 10. Гранулированные материалы........................ 205

10.1. Гранулированные материалы......................................... 205

10.2 Кулоновская блокада и переход металл-изолятор....... 212

11. Список литературы......................................................... 221

ВВЕДЕНИЕ

Высшей степенью пространственного порядка (кроме вакуума) является бесконечный кристалл. Ансамбль идентичных атомов заполняющих кристалл, обладающий трансляционный симметрией.

Наличие беспорядка разрушает симметрию кристалла, т.е. приводит к отсутствию трансляционной инвариантности.

Последовательность построения и изучения физики идеального твердого тела (ФИТТ) при наличии трансляционной симметрии обычно содержит три раздела:

1. Метрика, которая определяется геометрией решетки (ячейкой Вигнера-Зейтца – рис.1. а). Полная метрика определяется симметрией решетки (теория групп). Прямая решетка определяет обратную решетку в k-пространстве и зону Брюэллена.

2. Термодинамические свойства твердого тела – это возбуждения, связанные с малыми отклонениями от трансляционной симметрии: фононы; электроны, магноны и т.п., имеющие термодинамические функции распределения. Спектр возбуждений находится для электронов, например, в задаче Кронига-Пенни:

Все значения вектора k в обратном пространстве принадлежат зоне Брюэллена. Поверхность Ферми – энергетическая поверхность в k пространстве, ограничивающая все занятые состояния.

3. Кинетические характеристики - слабые отклонения от равновесия – теплопроводность, электропроводность.

В отсутствии дальнего порядка все представления, отталкивающиеся от трансляционной симметрии, должны разрушаться. Например, простейшая физическая картина – картина дифракции когерентных плоских волн на Брэговских плоскостях кристалла теряет смысл – при рассеянии волн с длиной волны порядка межатомного расстояния вместо резких максимумов под определенными углами наблюдается так называемое гало – фон. Тем не менее, остатки трансляционной симметрии дают о себе знать в виде размытых максимумов.

Какие представления удается использовать при наличии беспорядка? Системы описываются вероятностными распределениями, но не произвольными. Есть свои ограничения:

1. Поскольку рассматриваются конденсированные системы, то большинство неупорядоченных систем имеют структуры близкие к плотной упаковке. Это следует из того, что структуры строятся из принципа геометрических ограничений атомов и химических связей. В результате: симметрии у полиэдра Вороного нет, но он имеет такой же объем, как ячейка Вигнера-Зейтца (Рис. 1.). Число ближайших соседей Z₁ остается приблизительно таким же, как у упорядоченных систем.

2. Любой конечный макро объем твердого тела может быть заменен другим объемом твердого тела. На определенных расстояниях плотность среды приблизительно постоянна. Любой ограниченный объем (10² - 10³ атомов – так называемых физически представительный объем) можно взять из любой части образца. Следовательно, исследуемая система является статистически однородной. Трансляция на такое расстояние возможна, т.е. импульс для достаточно длинных волн - достаточно хорошее квантовое число.

Виды беспорядка в конденсированных системах:

Ячеистый беспорядок – возникает в той ситуации, когда узлы решетки остаются в исходных положениях, но атомы в узлах случайно замещаются атомами другого сорта. Пример – сплав замещения – трансляция на вектор l дает попадание на узел решетки, но не обязательно на такой же атом.

Топологический беспорядок – сорт атомов может не меняться, но атомы статически или динамически смещены из узлов решетки. Пример – жидкость. Ближний порядок может иметь место, но дальнего порядка и трансляционной симметрии – нет.

Континуальный беспорядок – такая модель возникает в случае, если удается использовать континуальное представление о веществе, то есть, если игнорировать атомную структуру вещества. Пример - атмосфера, океан, флуктуации плотности которых имеют размер значительно больший межатомного расстояния.

 

 

Рис. 1. а – ячейка Вигнера-Зейтца для идеальной решетки;

б – полиэдр Вороного для неупорядоченной системы

V_ВЗ ≈ V_{Вороного,} Z₁ ≈ Z_{1Вороного}