Размер и области упорядочения и упорядоченные домены
Из предыдущего следует, что числа заполнения узлов замещаемой решетки не полностью определяются параметрами ближнего и дальнего порядков (2.6, 2.7 и 2.16). Система, в которой происходят кооперативные явления, обладает следующим характерным свойством: даже очень короткодействующие силы могут привести к распространению порядка на довольно большие расстояния. Однако, надо сказать, что при данной температуре эти расстояния могут быть и не бесконечно большими. Для описания таких состояний с промежуточным порядком необходимо изучить поведение корреляционной функции
Рис. 2.13. Функция Г(R) - характеристика ближнего порядка, рассчитанная для последовательных координационных сфер в бинарном сплаве. Кривая хорошо описывается плавной функцией вида (2.17)
Показатель степени n зависит от размерности решетки и от природы сил взаимодействия; главную роль, однако, здесь играет показательная функция, которая очень быстро убывает на расстояниях, превышающих корреляционную длину x. Последняя величина, или связанная с ней длина L, определяемая соотношением
как раз и характеризует размер области упорядочения в рассматриваемом материале. Таким образом, температурная зависимость x описывает изменение «хаотичности» магнитной системы или сплава. При очень высоких температурах, когда x стремится к нулю, рассматриваемый ансамбль совершенно неупорядочен. При понижении температуры возникает ближний порядок (в пределах одной – двух постоянных решетки). При более низких температурах величина x становится очень большой и описывает критические флуктуации спина или концентрации. Температура, при которой длина x обращается в бесконечность, соответствует установлению дальнего порядка - это есть критическая температура перехода порядок – беспорядок Размер области упорядочения можно непосредственно измерить дифракционными методами. Температурная зависимость корреляционной длины x вблизи температуры Вместе с тем одной лишь скалярной корреляционной функции (7) еще не достаточно для описания локального порядка в классической системе спиновых векторов. Пусть, например, величина В действительности интересующая нас информация содержится в двухузелъной функции распределения
Рис. 2.14. Одно и то же значение локального параметра
Даже в простейшем случае, когда эта вероятность зависит только от угла
Т.е. функция корреляции Г (R), представляющая собой интеграл При температурах, близких к Как это ни парадоксально, но, обратившись к изучению упорядоченных доменов, мы можем вместе с тем убедиться, что почти каждый атом принадлежит бесконечному домену с идеальным АB -упорядочением (рис. 2.15).
Рис. 2.15. К чему относится выделенный атом: к кластеру, состоящему из атомов только типа А, или к области идеального порядка типа АВ.
Такие «кластеры» или «домены» взаимно проникают друг в друга, образуя очень сложную топологическую структуру. Бесконечная система полностью описывается только значением функционалом распределения бесконечного порядка. Для описания доменной границы нужно знать как минимум 4-х частичную функцию распределения
Рис.2.16. Температурная зависимость параметров типичного ферромагнетика:
|

 в зависимости от расстояния между узлами решетки (рис.2.13). Как мы увидим в дальнейшем, различные теории критических явлений приводят к различным типам зависимости этой функции от расстояния R, температуры и обменного параметра J. На больших расстояниях, однако, всегда получаются выражения вида
в зависимости от расстояния между узлами решетки (рис.2.13). Как мы увидим в дальнейшем, различные теории критических явлений приводят к различным типам зависимости этой функции от расстояния R, температуры и обменного параметра J. На больших расстояниях, однако, всегда получаются выражения вида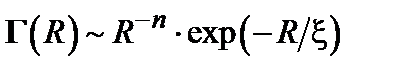 (2.17)
(2.17)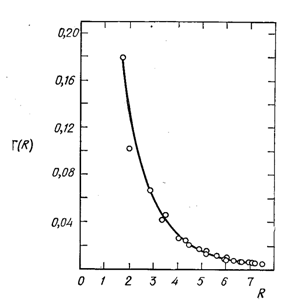
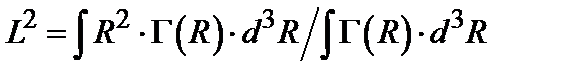 , (2.18)
, (2.18)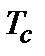 (в ферромагнетике это температура Кюри, в антиферромагнетике - температура Нееля). При температурах ниже
(в ферромагнетике это температура Кюри, в антиферромагнетике - температура Нееля). При температурах ниже 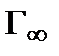 оказывается, отличным от нуля, и система находится в упорядоченном состоянии.
оказывается, отличным от нуля, и система находится в упорядоченном состоянии.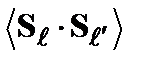 . Зная только это, нельзя сделать выбор между двумя возможностями: указанный эффект может быть обусловлен либо тем, что в системе есть лишь малое число соседних атомов с перевернутыми спинами, либо тем, что спины всех соседних узлов слегка отклонились от направления вектора
. Зная только это, нельзя сделать выбор между двумя возможностями: указанный эффект может быть обусловлен либо тем, что в системе есть лишь малое число соседних атомов с перевернутыми спинами, либо тем, что спины всех соседних узлов слегка отклонились от направления вектора 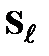 (рис. 2.14).
(рис. 2.14).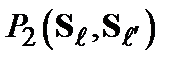 . Последняя определяет вероятность найти два спина
. Последняя определяет вероятность найти два спина 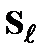 и
и 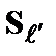 в двух указанных узлах, принадлежащих любой системе из данного ансамбля.
в двух указанных узлах, принадлежащих любой системе из данного ансамбля.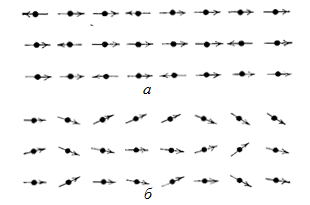
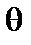 между направлениями спинов, корреляционная функция дает нам лишь среднее значение cosq:
между направлениями спинов, корреляционная функция дает нам лишь среднее значение cosq: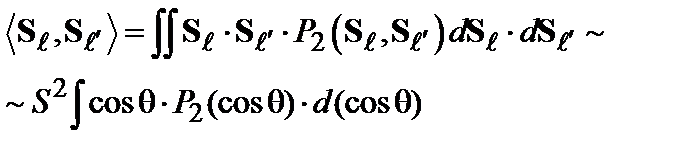 . (2.19)
. (2.19)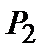 , содержит менее подробное описание системы, чем функция
, содержит менее подробное описание системы, чем функция 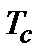 , когда размер области упорядочения достаточно велик, длину x можно рассматривать как характерный размер кластера одинаковых атомов или упорядоченного домена. Однако при более скромной степени локального порядка ошибочно представлять себе образец как совокупность упорядоченных областей в неупорядоченной матрице.
, когда размер области упорядочения достаточно велик, длину x можно рассматривать как характерный размер кластера одинаковых атомов или упорядоченного домена. Однако при более скромной степени локального порядка ошибочно представлять себе образец как совокупность упорядоченных областей в неупорядоченной матрице.
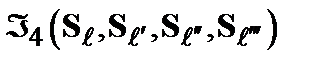 .
.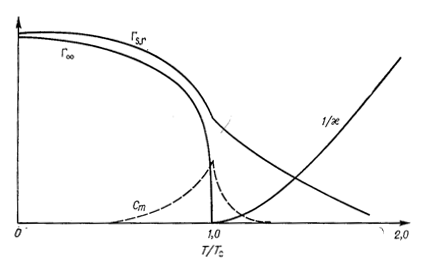
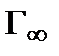 - параметр дальнего порядка;
- параметр дальнего порядка; 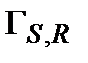 – параметр ближнего порядка;
– параметр ближнего порядка; 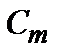 – удельная теплоемкость, c - восприимчивость.
– удельная теплоемкость, c - восприимчивость.


