Ближний порядок и корреляции
Основной недостаток приближения среднего поля – полное пренебрежение корреляциями между спинами на соседних узлах. Это особенно существенно чуть выше критической точки, так как выше рассмотренное приближение не позволяет принять во внимание возрастание размеров областей упорядоченности. Отсюда, например, теплоемкость системы в этом приближении при Т > Т 0 равна нулю. Оценим данную корреляцию. Приближение 0. Рассмотрим изолированную пару изинговых спинов s1 и s2, прямое взаимодействие между которыми равно J 12. Среднее по ансамблю 2-х спинов
Возможные конфигурации, по которым проводится суммирование, показаны ниже: ¯ ¯ ¯ ¯ 1 2 3 4 Для этой простой системы двух спинов полная коррекция совпадает с прямой. Приближение 1 Рассмотрим системы спинов (т.е. число спинов отлично от двух), обобщая выражение для эффективного поля. А именно, вычислим «эффективный обменный интеграл» J эф(1, 2) между спином s1, находящимся в узле 1, и спином s2, находящимся в соседнем узле. Поле, действующее на спин 1, обусловлено как прямым взаимодействием со спином s2, так и всеми эффектами, обусловленными другими спинами s k (k ¹ 1, 2), в известной мере «поляризованными» спинами s1 и s2. Можно записать для спина 1
Будем считать
Учитывая это приближение и умножив равенство (2.24) на спин
Мы отделили спины
Заменяя
Поскольку Пусть kT > > J, раскладывая Arth по малому параметру, получим:
Если использовать приближение
Здесь игнорируется возможное влияние величины
Это уравнение уже является линейным, описывающим распространение параметра ближнего порядка
Нам нужно найти Г корреляционную функцию. Поскольку все вышесказанное относится к ячеистому беспорядку, то введем Фурье-преобразование
Обратное преобразование определим как
Исходное уравнение
преобразуется в уравнение для фурье-образов
Если снять ограничение
тогда уравнение для Фурье-образов преобразуется
Спектральная плотность флуктуаций связанна с корреляциями ближнего порядка для малых q. Пусть
тогда
где
Рис. 2.18. Температурная зависимость длины когерентности
Обратное преобразование Фурье дает корреляционную функцию
Это выражение легко получить преобразованием
Выражение для корреляционной функции может быть распространено на случай дальнего порядка Z ¹ 0:
но меняется корреляционная длина:
где Z (T) - дальний порядок.
|

 . (2.23)
. (2.23)
 (2.24)
(2.24) только для ближайших соседей к узлу 1. Заменим
только для ближайших соседей к узлу 1. Заменим  . Такая замена относится только к третьим соседям, т.е. не 1 и 2 - приближение по косвенным корреляциям. Чтобы придать величине
. Такая замена относится только к третьим соседям, т.е. не 1 и 2 - приближение по косвенным корреляциям. Чтобы придать величине  точный смысл, надо ввести функции распределения спинов
точный смысл, надо ввести функции распределения спинов  ,
,  и т. д., с учетом прежде всего вероятности
и т. д., с учетом прежде всего вероятности  найти данные значения спина
найти данные значения спина  и определить интересующее нас среднее равенством
и определить интересующее нас среднее равенством
 , найдем обменный интеграл
, найдем обменный интеграл 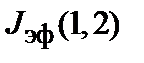 :
:
 и
и  надо понимать тот самый обменный параметр
надо понимать тот самый обменный параметр 
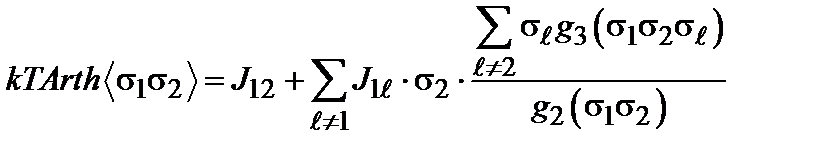 . (2.25)
. (2.25) , то уравнение было бы замкнутым, если бы
, то уравнение было бы замкнутым, если бы  ,
,  были известны. Можно было бы посмотреть еще более высокую цепочку уравнений, связывающую
были известны. Можно было бы посмотреть еще более высокую цепочку уравнений, связывающую 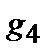 .
. . (2.26)
. (2.26)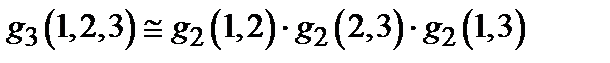 (это приближение из теории вероятностей), то получим нелинейное уравнение. Применим еще более грубое приближение:
(это приближение из теории вероятностей), то получим нелинейное уравнение. Применим еще более грубое приближение: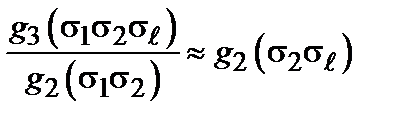 (2.27)
(2.27)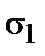 на корреляцию между спинами
на корреляцию между спинами  и
и  . В отсутствие дальнего порядка можно линеаризовать левую часть формулы (2.26), при этом получается соотношение
. В отсутствие дальнего порядка можно линеаризовать левую часть формулы (2.26), при этом получается соотношение (2.28)
(2.28) . Последнее условие - приближение однородного поля, т.е. все определяется разностью координат. Тогда получим замкнутое уравнение
. Последнее условие - приближение однородного поля, т.е. все определяется разностью координат. Тогда получим замкнутое уравнение , (2.29)
, (2.29)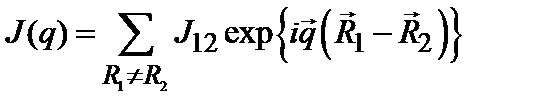 ,
, . (2.30)
. (2.30) .
.

 в соответствующей сумме, то появившееся дополнительное слагаемое с
в соответствующей сумме, то появившееся дополнительное слагаемое с  просто будет постоянным, т.к. при Т ® Т с длина корреляции x возрастает, а радиус соответствующего интеграла перекрытия
просто будет постоянным, т.к. при Т ® Т с длина корреляции x возрастает, а радиус соответствующего интеграла перекрытия  остается постоянным.. Влиянием этого добавленного постоянного слагаемого можно пренебречь. Двойную сумму можно разбить на две части:
остается постоянным.. Влиянием этого добавленного постоянного слагаемого можно пренебречь. Двойную сумму можно разбить на две части: , (2.31)
, (2.31) ,
,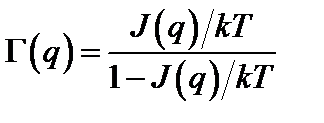 . (2.32)
. (2.32) - радиус ближайших соседей. Поскольку взаимодействие локализовано и распространяется только на ближайших соседей, представим его в виде:
- радиус ближайших соседей. Поскольку взаимодействие локализовано и распространяется только на ближайших соседей, представим его в виде: ,
, , (2.33)
, (2.33) , а - параметр решетки (рис.2.18).
, а - параметр решетки (рис.2.18).
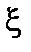
 . (2.34)
. (2.34) .
. ,
, , (2.35)
, (2.35)


