Напомним сначала понятие однородной функции двух переменных.
Определение. Функция  называется однородной функцией k -го измерения (степени k), если для всех t выполняется соотношение
называется однородной функцией k -го измерения (степени k), если для всех t выполняется соотношение
 .
.
Например, функция  однородная функция 2-го измерения, так как
однородная функция 2-го измерения, так как
 ,
,
а функция  однородная функция нулевого измерения,
однородная функция нулевого измерения,
ибо
 .
.
Определение. Уравнение
 , (1.21)
, (1.21)
где 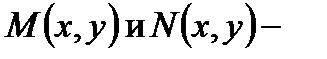 однородные функции одного и того же измерения, называется однородным.
однородные функции одного и того же измерения, называется однородным.
Однородное уравнение всегда приводится к виду
 , (1.22)
, (1.22)
где  функция одной переменной, т.е. правая часть (1.22) есть однородная функция нулевого измерения.
функция одной переменной, т.е. правая часть (1.22) есть однородная функция нулевого измерения.
Однородное уравнение интегрируется посредством подстановки  , где
, где  новая неизвестная функция переменной х, то есть
новая неизвестная функция переменной х, то есть  .
.
Пример 1. Проинтегрировать уравнение
 . (1.23)
. (1.23)
Решение. Здесь функции  и
и  - однородные функции первого измерения, так как
- однородные функции первого измерения, так как
 ,
,
 .
.
Следовательно, (1.23) - однородное ОДУ. Положим  , тогда
, тогда  . Подставим
. Подставим  и
и  в (1.23), будем иметь
в (1.23), будем иметь
 ,
,
 ,
,
 . (1.24)
. (1.24)
Уравнение (1.24) –это уравнение с разделяющимися переменными. Умножением обеих частей на  приведем его к уравнению с разделенными переменными
приведем его к уравнению с разделенными переменными
 .
.
Последнее имеет общее решение
 ,
,
следовательно, при  общее решение уравнения (1.23) есть
общее решение уравнения (1.23) есть
 . (1.25)
. (1.25)
Заметим, что функция  является решением (1.23). Она является частным решением рассматриваемого уравнения, так как соответствующие ей полупрямые лежат в областях существования и единственности уравнения
является решением (1.23). Она является частным решением рассматриваемого уравнения, так как соответствующие ей полупрямые лежат в областях существования и единственности уравнения
 ,
,
получающегося из (1.23) разрешением относительно  . Решение
. Решение  не входит в формулу (1.25) ни при каком конечном значении произвольной константы С, т.е. оно оказалось потерянным.
не входит в формулу (1.25) ни при каком конечном значении произвольной константы С, т.е. оно оказалось потерянным.
Пример 2. Найти общий интеграл уравнения
 . (1.26)
. (1.26)
Решение. ОДУ (1.26) - однородное, так как правая часть его является однородной функцией нулевого измерения. Полагая  , где
, где  новая неизвестная функция от
новая неизвестная функция от  , найдем
, найдем  . Подставляя
. Подставляя  и
и  в уравнение (1.26), получим
в уравнение (1.26), получим
 ,
,
 ,
,
 . (1.27)
. (1.27)
Уравнение (1.27) – это уравнение с разделяющимися переменными. Разделяя переменные, приведем его к виду
 .
.
Общим интегралом последнего уравнения является соотношение
 ,
,
следовательно, общим интегралом уравнения (1.26) будет соотношение
 .
.
При интегрировании (1.27) мы считали  , поэтому остается проверить, не являются ли полупрямые
, поэтому остается проверить, не являются ли полупрямые  интегральными кривыми ОДУ (1.26). Подставляя
интегральными кривыми ОДУ (1.26). Подставляя  в (1.26) убедимся в том, что эта функция рассматриваемому уравнению не удовлетворяет.
в (1.26) убедимся в том, что эта функция рассматриваемому уравнению не удовлетворяет.

 называется однородной функцией k -го измерения (степени k), если для всех t выполняется соотношение
называется однородной функцией k -го измерения (степени k), если для всех t выполняется соотношение .
. однородная функция 2-го измерения, так как
однородная функция 2-го измерения, так как ,
, однородная функция нулевого измерения,
однородная функция нулевого измерения, .
. , (1.21)
, (1.21)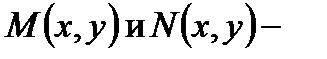 однородные функции одного и того же измерения, называется однородным.
однородные функции одного и того же измерения, называется однородным. , (1.22)
, (1.22) функция одной переменной, т.е. правая часть (1.22) есть однородная функция нулевого измерения.
функция одной переменной, т.е. правая часть (1.22) есть однородная функция нулевого измерения. , где
, где  новая неизвестная функция переменной х, то есть
новая неизвестная функция переменной х, то есть  .
. . (1.23)
. (1.23) и
и  - однородные функции первого измерения, так как
- однородные функции первого измерения, так как ,
, .
. , тогда
, тогда  . Подставим
. Подставим  и
и  в (1.23), будем иметь
в (1.23), будем иметь ,
, ,
, . (1.24)
. (1.24) приведем его к уравнению с разделенными переменными
приведем его к уравнению с разделенными переменными .
. ,
, общее решение уравнения (1.23) есть
общее решение уравнения (1.23) есть . (1.25)
. (1.25) является решением (1.23). Она является частным решением рассматриваемого уравнения, так как соответствующие ей полупрямые лежат в областях существования и единственности уравнения
является решением (1.23). Она является частным решением рассматриваемого уравнения, так как соответствующие ей полупрямые лежат в областях существования и единственности уравнения ,
, . Решение
. Решение  не входит в формулу (1.25) ни при каком конечном значении произвольной константы С, т.е. оно оказалось потерянным.
не входит в формулу (1.25) ни при каком конечном значении произвольной константы С, т.е. оно оказалось потерянным. . (1.26)
. (1.26) , где
, где  новая неизвестная функция от
новая неизвестная функция от  , найдем
, найдем  . Подставляя
. Подставляя  и
и  в уравнение (1.26), получим
в уравнение (1.26), получим ,
, ,
, . (1.27)
. (1.27) .
. ,
, .
. , поэтому остается проверить, не являются ли полупрямые
, поэтому остается проверить, не являются ли полупрямые  интегральными кривыми ОДУ (1.26). Подставляя
интегральными кривыми ОДУ (1.26). Подставляя  в (1.26) убедимся в том, что эта функция рассматриваемому уравнению не удовлетворяет.
в (1.26) убедимся в том, что эта функция рассматриваемому уравнению не удовлетворяет.


