Определение. Обыкновенным дифференциальным уравнением (ОДУ) первого порядка называется уравнение вида
 , (1.1)
, (1.1)
где  - независимая переменная;
- независимая переменная;  - искомая функция этой переменной;
- искомая функция этой переменной; 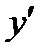 - производная от
- производная от  по
по  ;
;  - заданная функция своих аргументов.
- заданная функция своих аргументов.
Определение. Непрерывно дифференцируемая на некотором интервале 
 функция
функция  , которая при подстановке в уравнение (1.1) обращает его в тождество по
, которая при подстановке в уравнение (1.1) обращает его в тождество по  на
на 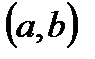 , называется решением этого уравнения.
, называется решением этого уравнения.
График решения  ОДУ (1.1) есть его интегральная кривая.
ОДУ (1.1) есть его интегральная кривая.
Если уравнение (1.1) удается записать в виде
 , (1.2)
, (1.2)
то последнее называют ОДУ, разрешенным относительно производной. В настоящем учебном пособии рассматриваются именно такие уравнения.
Часть  плоскости
плоскости  , в которой функция
, в которой функция 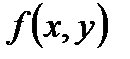 непрерывна, называется областью задания ОДУ (1.2).
непрерывна, называется областью задания ОДУ (1.2).
Определение. Задачей Коши для уравнения (1.2) называется задача отыскания решения  этого уравнения, удовлетворяющего условию
этого уравнения, удовлетворяющего условию
 . (1.3)
. (1.3)
Условие (1.3) – начальное условие, а числа  - начальные данные задачи Коши.
- начальные данные задачи Коши.
Геометрическая интерпретация задачи Коши – найти интегральную кривую ОДУ (1.2), проходящую через точку  .
.
Говорят, что решение задачи Коши для уравнения (1.2) с начальным условием (1.3) единственно, если существует такая окрестность точки  , что
, что
1) в этой окрестности определено решение с начальными данными  ;
;
2) не существует другого решения с начальными данными  , определенного в той же окрестности.
, определенного в той же окрестности.
Имеет место следующая теорема существования и единственности решения задачи Коши.
Теорема. Если в области  плоскости
плоскости 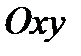 функция
функция 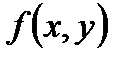 и ее частная производная
и ее частная производная  непрерывны по совокупности аргументов, то существует единственное решение
непрерывны по совокупности аргументов, то существует единственное решение  уравнения (1.2), удовлетворяющее начальному условию
уравнения (1.2), удовлетворяющее начальному условию
 .
.
Пусть  есть область в плоскости
есть область в плоскости  , через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения.
, через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения.
Определение. Функция  , (1.4)
, (1.4)
пределенная в некоторой области изменения переменных  и
и  и непрерывно дифференцируемая по
и непрерывно дифференцируемая по  , называется общим решением уравнения (1.2) в области
, называется общим решением уравнения (1.2) в области 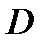 , если
, если
1) равенство (1.4) разрешимо в  относительно
относительно  :
:
 , (1.5)
, (1.5)
2) функция (1.4) является решением ОДУ (1.2) при всех значениях  , определяемых формулой (1.5), когда точка
, определяемых формулой (1.5), когда точка  пробегает
пробегает
область  .
.
Переменная 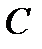 в (1.4) называется произвольной постоянной (константой).
в (1.4) называется произвольной постоянной (константой).
Определение. Равенство  , неявно задающее общее решение, называется общим интегралом ОДУ (1.2).
, неявно задающее общее решение, называется общим интегралом ОДУ (1.2).
Решение  уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку
уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку  такой кривой проходит единственная интегральная кривая уравнения (1.2).
такой кривой проходит единственная интегральная кривая уравнения (1.2).
Определение. Решение  , получающееся из общего решения (1.4) фиксированием произвольной константы
, получающееся из общего решения (1.4) фиксированием произвольной константы  , есть частное решение.
, есть частное решение.
Определение. Говорят, что решение  уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши.
уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши.
Если функция  , в правой части ОДУ (1.2) непрерывна по
, в правой части ОДУ (1.2) непрерывна по  и имеет частную производную по
и имеет частную производную по  (ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых
(ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых
 .
.
Если в некоторых точках плоскости  функция
функция  обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение
обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение
 , (1.6)
, (1.6)
в котором считают  функцией от
функцией от  . Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения
. Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения  уравнения (1.6) – к решениям ОДУ (1.2).
уравнения (1.6) – к решениям ОДУ (1.2).
Уравнениям (1.2) и (1.6) равносильно ОДУ первого порядка в дифференциальной форме вида
 . (1.7)
. (1.7)
Оно не задано в тех точках  , где непрерывные функции
, где непрерывные функции  и
и  обращаются в нуль одновременно. В уравнение (1.7) переменные
обращаются в нуль одновременно. В уравнение (1.7) переменные  и
и  входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину
входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину  как функцию от
как функцию от  .
.
Ниже в пунктах 1.2 – 1.6 рассматриваются различные типы дифференциальных уравнений первого порядка, разрешенных относительно производной, и методы их решения.

 , (1.1)
, (1.1) - независимая переменная;
- независимая переменная;  - искомая функция этой переменной;
- искомая функция этой переменной; 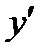 - производная от
- производная от  по
по  ;
;  - заданная функция своих аргументов.
- заданная функция своих аргументов.
 функция
функция  , которая при подстановке в уравнение (1.1) обращает его в тождество по
, которая при подстановке в уравнение (1.1) обращает его в тождество по  на
на 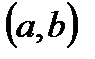 , называется решением этого уравнения.
, называется решением этого уравнения. ОДУ (1.1) есть его интегральная кривая.
ОДУ (1.1) есть его интегральная кривая. , (1.2)
, (1.2) плоскости
плоскости  , в которой функция
, в которой функция 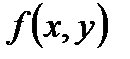 непрерывна, называется областью задания ОДУ (1.2).
непрерывна, называется областью задания ОДУ (1.2). этого уравнения, удовлетворяющего условию
этого уравнения, удовлетворяющего условию . (1.3)
. (1.3) - начальные данные задачи Коши.
- начальные данные задачи Коши. .
. , что
, что ;
; , определенного в той же окрестности.
, определенного в той же окрестности. плоскости
плоскости 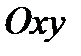 функция
функция 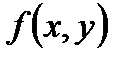 и ее частная производная
и ее частная производная  непрерывны по совокупности аргументов, то существует единственное решение
непрерывны по совокупности аргументов, то существует единственное решение  уравнения (1.2), удовлетворяющее начальному условию
уравнения (1.2), удовлетворяющее начальному условию .
. есть область в плоскости
есть область в плоскости  , через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения.
, через каждую точку которой проходит одна и только одна интегральная кривая ОДУ (1.2). В дальнейшем такую область условимся называть областью существования и единственности решения задачи Коши или, более кратко, областью существования и единственности рассматриваемого уравнения. , (1.4)
, (1.4) и
и  и непрерывно дифференцируемая по
и непрерывно дифференцируемая по  , называется общим решением уравнения (1.2) в области
, называется общим решением уравнения (1.2) в области 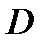 , если
, если относительно
относительно  :
: , (1.5)
, (1.5) , определяемых формулой (1.5), когда точка
, определяемых формулой (1.5), когда точка  пробегает
пробегает .
.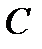 в (1.4) называется произвольной постоянной (константой).
в (1.4) называется произвольной постоянной (константой). , неявно задающее общее решение, называется общим интегралом ОДУ (1.2).
, неявно задающее общее решение, называется общим интегралом ОДУ (1.2). уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку
уравнения (1.2) называется частным, если в каждой точке соответствующей ему интегральной кривой сохраняется единственность решения задачи Коши. Через каждую точку  такой кривой проходит единственная интегральная кривая уравнения (1.2).
такой кривой проходит единственная интегральная кривая уравнения (1.2). , получающееся из общего решения (1.4) фиксированием произвольной константы
, получающееся из общего решения (1.4) фиксированием произвольной константы  , есть частное решение.
, есть частное решение. уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши.
уравнения (1.2) особое, если в каждой точке соответствующей ему интегральной кривой нарушается единственность решения задачи Коши. , в правой части ОДУ (1.2) непрерывна по
, в правой части ОДУ (1.2) непрерывна по  и имеет частную производную по
и имеет частную производную по  (ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых
(ограниченную или нет), то особыми решениями могут быть только те кривые, во всех точках которых .
. функция
функция  обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение
обращается в бесконечность, то в окрестности таких точек рассматривают перевернутое по отношению к (1.2) уравнение , (1.6)
, (1.6) функцией от
функцией от  . Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения
. Совокупность таких точек присоединяют к области задания уравнения (1.2), а решения  уравнения (1.6) – к решениям ОДУ (1.2).
уравнения (1.6) – к решениям ОДУ (1.2). . (1.7)
. (1.7) , где непрерывные функции
, где непрерывные функции  и
и  обращаются в нуль одновременно. В уравнение (1.7) переменные
обращаются в нуль одновременно. В уравнение (1.7) переменные  и
и  входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину
входят равноправно. При решении конкретных уравнений вида (1.7) часто бывает удобно в отличие от традиционных обозначений рассматривать переменную величину  как функцию от
как функцию от  .
.


