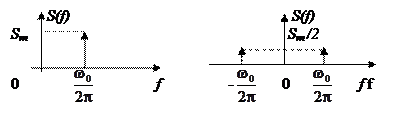Частотный спектр
Сигналы, которые применяются в современных системах связи, имеют сложный вид, но в большинстве случаев работу любой системы связи можно проанализировать, используя в качестве базового сигнала простой синусоидальный сигнал S(t) вида (1.2), который описывает гармоническое колебание. Совокупность простых гармонических колебаний, на которые может быть разложен сложный сигнал, называется частотнымспектром сигнала. Для описания частотного спектра сигнала используется ряд Фурье. Совокупность амплитуд гармоник ряда Фурье называют амплитудным спектром, а совокупность начальных фаз – фазовым спектром. Эти понятия не следует путать с амплитудно– и фазочастотными характеристиками, которые относятся к цепям, а не сигналам. Как уже было сказано, для передачи сигнал предварительно необходимо преобразовать в вид, приемлемый для передачи по каналу связи. Ключевой операцией здесь является изменение его спектральных свойств или его частотного спектра. Эта операция применяется для согласования частотного спектра сигнала с характеристиками канала связи. В некоторых системах связи сигналы с данным частотным спектром могут непосредственно подаваться на вход канала связи без модуляции несущей. Такая передача называется передачей модулирующего сигнала или передача видеосигнала. В радио или оптоволоконных линиях связи частотный спектр исходного сигнала отличается от частотного спектра, который можно непосредственно передать по каналу. В таких случаях необходимо перенести частотный спектр сигнала в область более высоких частот. Перенос частотного спектра называется преобразованием. Чтобы определить, соответствует ли частотный спектр сигнала полосе пропускания канала связи, необходимо сначала определить частотный спектр сигнала. Существует ряд «стандартных» простых сигналов, спектр которых хорошо известен. Для определения спектра других сигналов необходимо использовать специальные методы. Рассмотренный в (1.2) простой синусоидальный сигнал, описывается функцией Кроме представления во временной области (рисунок 3.1, а) сигнал представляется в частотной области (рисунок 3.1, б). По вертикальной оси на этом графике откладывается амплитуда, а по горизонтальной – частота. Спектр имеет только одну составляющую, которая описывается δ –импульсом. Такой спектр будет называться линейчатым. Энергия частотного спектра сосредоточена на одной дискретной частоте. В случае такого распределения частотных составляющих сигнала его временное представление имеет вид непрерывной функции. При этом аргумент функции S(t) – время изменяется в бесконечных пределах.
Если сигнал является периодическим, то спектр такого сигнала математически представляется рядом Фурье. Спектр непериодического сигнала определяется с помощью интеграла Фурье, примененного к функции, описывающей временное представление сигнала.
|
, которая содержит только одну гармоническую компоненту с частотой 
(Гц).
