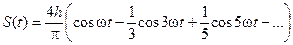Задачи по разделу 3
Пример 1. Представить ряд Фурье и определить спектр периодического сигнала, представленного на рисунке 3.12, имеющего амплитуду h, период Т 0 и длительность импульсов τ.
Рисунок 3.12 – Периодический сигнал 1) Подставляем исходные данные в выражение комплексной амплитуды частоты спектра (3.15):
Используя табличный интеграл
Таким образом, частотный спектр периодической последовательности прямоугольных импульсов в виде ряда Фурье запишется как:
Из (3.27) следует, что огибающая амплитудного спектра соответствует амплитуде спектра одиночного импульса (3.16). Эта огибающая изображена штриховой линией на рисунке 3.13. 2) Для определения спектральных составляющих ak и bk воспользуемся выражением (3.4). Из графика видно, что среднее значение функции или постоянная составляющая сигнала а0 = 0 В. Запишем выражение для функции S(t) на длине одного периода Т:
Определим косинусоидальные составляющие ряда Фурье:
Поскольку T =2 π /ω, то sinkω T = sink2π =0, поэтому это выражение можно записать как:
Отсюда
Теперь определим синусоидальные составляющие сигнала:
где В итоге выражение для функции S(t) согласно (3.8) принимает следующий вид:
Спектр этого сигнала представлен на рисунке 3.13.
Рисунок 3.13 – Частотный спектр периодической импульсной последовательности
Пример 2. Найти спектр амплитуд периодической последовательности импульсов с амплитудой U=10B, периодом T0=10мс и длительностью τ =5мс.
|


 ;
; , получим:
, получим: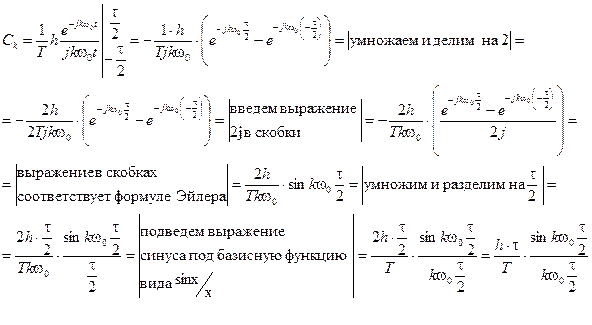
 . (3.27)
. (3.27)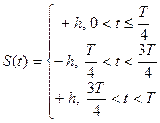




 , следовательно,
, следовательно,  . Таким образом, спектр данного сигнала имеет только косинусоидальные составляющие, синусоидальные составляющие равны нулю, отсутствует и постоянная составляющая. Присутствуют только косинусоидальные составляющие только нечетных гармоник.
. Таким образом, спектр данного сигнала имеет только косинусоидальные составляющие, синусоидальные составляющие равны нулю, отсутствует и постоянная составляющая. Присутствуют только косинусоидальные составляющие только нечетных гармоник.