Решение. 1) Запишем формулу для спектра амплитуд:
1) Запишем формулу для спектра амплитуд: 2) Подставим заданные значения:
где 3) По формуле определим значения для
C0=5В;
4) Определяем частоту ω 0:
Рисунок 3.14
Пример 3. Осуществить восстановление исходного сигнала по его спектру, используя для восстановления постоянную составляющую S0 =10 B гармоники со значениями комплексных амплитуд S1=5B, S2=0B, S3=-1, 06B, S4=0B. Частота первой гармоники
Суммирование членов ряда Фурье при восстановлении осуществить графическим методом. Оценить качество восстановления исходного сигнала при использовании только постоянной составляющей, постоянной составляющей и первой гармоники, постоянной составляющей и всех гармоник. Решение. Используя ряд Фурье (3.5), имеем:
а) при восстановлении исходного сигнала по постоянной составляющей имеем (т.к. по
Рисунок 3.15 б) при восстановлении исходного сигнала по сумме S0+ S1 имеем
Строим график (рисунок 3.16):
Рисунок 3.16 в) при восстановлении по сумме
Строим график:
Рисунок 3.17 Вывод: При большем числе гармоник результат восстановления получается лучше. При точном подсчете при использовании десяти гармоник сигнал принимает исходный вид.
Пример 4. Найти спектр
|
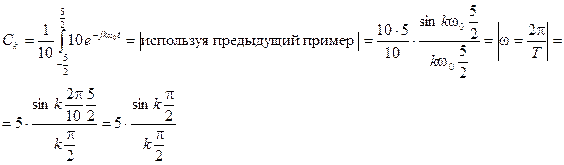
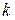– номера гармоник; 
.
:
; 
; 
; 
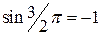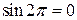
3, 2В;
.
): 
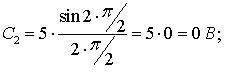
– не существенно.
; 
;
;
; (
)
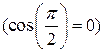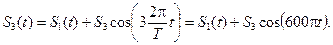
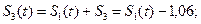
–функции, исходя из спектра одиночного прямоугольного импульса длительностью 
и амплитудой 
, при 
. Изобразить график 
