Энергия сигнала
На практике очень часто используются такие характеристики, как энергия и мощность сигнала. Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет равна
За время T в этом резисторе выделится тепловая энергия, равная
Пусть теперь к тому же резистору приложено не постоянное напряжение, а напряжение, описываемое сигналом S(t). Рассеивающаяся в резисторе мощность при этом тоже будет зависеть от времени. Тогда мгновенная мощность будет описываться выражением:
Чтобы вычислить выделяющуюся за время Т энергию, мгновенную мощность необходимо проинтегрировать в пределах интервала Т:
Можно ввести также понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:
Во все формулы входит сопротивление нагрузки R. Однако, если энергия и мощность интересуют нас не как физические величины, а как средство сравнения различных сигналов, этот параметр можно из формул исключить, приняв R =1 Ом. Тогда получим определение энергии, мгновенной мощности и средней мощности, принятые в теории сигналов:
фактически сигнал не производит работы и физически энергии нет, т.к. сигнал – это абстрактное понятие. Однако, формально, взяв квадрат от сигнала, мы говорим о мощности или об энергии сигнала, применяя формально эти характеристики к сигналу. В теории передачи информации, практическое значение имеет равенство Парсеваля, формально описывающее закон сохранения энергии, применительно к сигналам при переходе от временного представления сигнала S(t) к частотному Ф(jω). Для получения равенства Парсеваля выполним следующее: 1) запишем выражение для энергии сигнала S(t) в виде:
2) выразим энергию через спектральную плотности амплитуд, т.е. используем обратное преобразование Фурье (3.17):
Поскольку S(t) не зависит от ω, то внесем S(t) во второй интеграл:
В результате получим равенство Парсеваля:
Физический смысл: проявляется закон сохранения энергии сигнала. Энергия сигнала во временной области равна энергии спектра сигнала в частотной области. Энергия сигнала может быть конечной или бесконечной. Например, любой сигнал конечной длительности будет иметь конечную энергию (если он не содержит дельта-функций или ветвей, уходящих в бесконечность). А периодический сигнал имеет бесконечную энергию. Если энергия сигнала бесконечна, то можно определить его среднюю мощность на всей временной оси. Для этого выполняется предельный переход, устремив интервал усреднения в бесконечность:
Если взять квадратный корень из средней мощности, то это даст среднеквадратическое (действующее) значение или эффективное значение сигнала:
|

 (3.18)
(3.18) (3.19)
(3.19) (3.20)
(3.20) (3.21)
(3.21) (3.22)
(3.22) (3.23)
(3.23)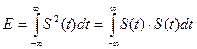 ;
; .
.
 . (3.24)
. (3.24) . (3.25)
. (3.25) . (3.26)
. (3.26)


