2.11.4.1 Межосевое расстояние (второе приближение):
 .
.
 = 410 для косозубых и шевронных зубчатых колес и
= 410 для косозубых и шевронных зубчатых колес и  = 450 для прямозубых зубчатых колес.
= 450 для прямозубых зубчатых колес.
Коэффициент ширины 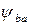 выбирают по табл. 2.7, в зависимости от положения зубчатых колес относительно опор.
выбирают по табл. 2.7, в зависимости от положения зубчатых колес относительно опор.
Коэффициент нагрузки 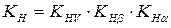 выбирают по рекомендациям п. 2.11.3.
выбирают по рекомендациям п. 2.11.3.
Допускаемое напряжение  выбирают в соответствии с рекомендациями п. 2.10.
выбирают в соответствии с рекомендациями п. 2.10.
Полученное значение 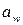 округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов
округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов 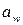 округляют до ближайшего стандартного значения: 63; 71; 80, 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400.
округляют до ближайшего стандартного значения: 63; 71; 80, 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400.
2.11.4.2 Ширина венца колеса равна рабочей ширине передачи, т.е.  .
.
Ширину венца шестерни принимают большую, чем у колеса, мм:  . Полученные значения
. Полученные значения 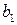 и
и  округляют до ближайших больших целых значений в миллиметрах.
округляют до ближайших больших целых значений в миллиметрах.
2.11.4.3 Нормальный модуль зубчатых колес определяют (с дальнейшим округлением по ГОСТ 9563-60) из следующих соотношений:
 ;
;  .
.
Значение коэффициента 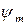 выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента
выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента 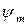 увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев.
увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев.
Таблица 2.8
Рекомендуемые значения 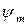
| Характеристика передачи
|  ,
не более ,
не более
|
| Обычные передачи в отдельном корпусе с достаточно жесткими валами и опорами, имеющие следующую твердость зубьев:
|
|
 и и  < 350 НВ < 350 НВ
| 30-25
|
 > 350 НВ и > 350 НВ и  < 350 HB < 350 HB
| 25-20
|
 и и  > 350 HB > 350 HB
| 20-15
|
 и и  > 58 HRC > 58 HRC
| 18-10
|
| Передачи грубые, открытые, с консольными валами и подвижные колеса коробок скоростей
| 15-10
|
Минимальный модуль  определяют из условия изгибной прочности колеса по следующей зависимости:
определяют из условия изгибной прочности колеса по следующей зависимости:
 ,
,
где  – коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач;
– коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач;
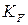 – коэффициент нагрузки принимаемый равным
– коэффициент нагрузки принимаемый равным  .
.
Допускаемое напряжение изгиба для колеса  определяют в п. 2.10.
определяют в п. 2.10.
Максимально допустимый модуль  определяют из условия неподрезания зубьев у основания:
определяют из условия неподрезания зубьев у основания:
 .
.
Полученное при расчете значение m округляют до ближайшего большего (согласно ГОСТ 9563-60), мм:
1-й ряд - 1; 1, 25; 1, 5; 2; 2, 5; 3; 4; 5; 6; 8; 10
2-й ряд - 1, 12; 1, 37; 1, 75; 2, 25; 2, 75; 3, 5; 4, 5; 5, 5; 7; 9
2.11.4.4 Суммарное число зубьев для прямозубых передач определяют по формуле:
 .
.
Учитывая, что  должно быть целым числом, иногда приходится изменять значения
должно быть целым числом, иногда приходится изменять значения 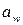 и m или осуществлять смещение инструмента (коррегирование зубьев).
и m или осуществлять смещение инструмента (коррегирование зубьев).
Для косозубых передач – минимальный угол наклона зубьев:
 .
.
Для шевронных передач угол  = 25°.
= 25°.
Затем определяют суммарное число зубьев по формуле:
 .
.
Полученное значение 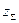 округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0, 0001):
округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0, 0001):
 ,
,  .
.
2.11.4.5 Числа зубьев шестерни  и колеса
и колеса  :
:
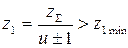
(значение  округляют до целого числа).
округляют до целого числа).
Для прямозубых и косозубых зубчатых колес, нарезанных без смещения инструмента ( =
=  =0),
=0),  = 17 и
= 17 и  соответственно.
соответственно.
Число зубьев колеса  для внешнего и внутреннего зацепления соответственно:
для внешнего и внутреннего зацепления соответственно:
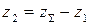 ,
,  .
.
2.11.4.6 Фактическое значение передаточного числа u с точностью до 0, 01:
 .
.
2.11.4.7 Определение геометрических параметров передачи:
делительный диаметр:  ;
;
диаметр вершин зубьев:  ;
;
диаметр впадин зубьев:  ;
;
2.11.4.8 Для расчета валов и подшипников определяют силы в зацеплении (рис. 2.9):
 ,
,
 ,
,
 ,
,
где  ,
,  и
и  – окружная, радиальная и осевая сила соответственно.
– окружная, радиальная и осевая сила соответственно.

 .
. = 410 для косозубых и шевронных зубчатых колес и
= 410 для косозубых и шевронных зубчатых колес и 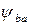 выбирают по табл. 2.7, в зависимости от положения зубчатых колес относительно опор.
выбирают по табл. 2.7, в зависимости от положения зубчатых колес относительно опор.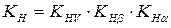 выбирают по рекомендациям п. 2.11.3.
выбирают по рекомендациям п. 2.11.3. выбирают в соответствии с рекомендациями п. 2.10.
выбирают в соответствии с рекомендациями п. 2.10.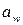 округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов
округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов  .
. . Полученные значения
. Полученные значения 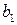 и
и  округляют до ближайших больших целых значений в миллиметрах.
округляют до ближайших больших целых значений в миллиметрах. ;
;  .
.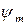 выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента
выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента 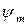 увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев.
увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев. ,
не более
,
не более
 и
и  < 350 НВ
< 350 НВ
 определяют из условия изгибной прочности колеса по следующей зависимости:
определяют из условия изгибной прочности колеса по следующей зависимости: ,
, – коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач;
– коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач;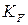 – коэффициент нагрузки принимаемый равным
– коэффициент нагрузки принимаемый равным  .
. определяют в п. 2.10.
определяют в п. 2.10. определяют из условия неподрезания зубьев у основания:
определяют из условия неподрезания зубьев у основания: .
. .
. должно быть целым числом, иногда приходится изменять значения
должно быть целым числом, иногда приходится изменять значения  .
. = 25°.
= 25°. .
.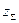 округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0, 0001):
округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0, 0001): ,
,  .
. и колеса
и колеса  :
: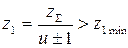
 =
=  =0),
=0),  = 17 и
= 17 и  соответственно.
соответственно.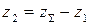 ,
,  .
. .
. ;
; ;
; ;
; ,
, ,
, ,
, ,
,  и
и  – окружная, радиальная и осевая сила соответственно.
– окружная, радиальная и осевая сила соответственно.


