Последовательность расчета. 3.7.2.1 Число витков червяка определяется в зависимости от передаточного числа: u до 14 свыше 14 до 30 свыше 30
3.7.2.1 Число витков
3.7.2.2 Межосевое расстояние, мм:
где
Начальный коэффициент концентрации нагрузки
Полученное расчетом межосевое расстояние округляют в большую сторону: для стандартной червячной пары – до стандартного числа из ряда (мм): 40, 50, 63, 80, 100, 125, 140, 160, 180, 200, 225, 250, 280, 315, 355, 400, 450, 500; для нестандартной – до числа из ряда нормальных линейных размеров (по ГОСТ 6636-69).
3.7.2.3 Основные параметры передачи (см. п. 3.3) Число зубьев колеса: Оптимальное значение Модуль передачи: Полученное значение модуля округляется до ближайшего стандартного значения (по ГОСТ 16672-74 и ГОСТ 2144-76): 1-й ряд – 2, 5; 3, 15; 4; 5; 6, 3; 8; 10; 12, 5; 16; 20; 25 2-й ряд – 3; 3, 5; 6; 7; 12; 14 1-й ряд следует предпочитать 2-му. Коэффициент диаметра червяка: Полученное значение q округляют до ближайшего стандартного (по ГОСТ 2144-76): 1-й ряд – 6, 3; 8; 10; 12, 5; 16; 20 2-й ряд – 7, 1; 9; 11, 2; 14; 18 1-й ряд следует предпочитать 2-му. Минимально допустимое значение q из условия жесткости червяка Коэффициент смещения:
Если по расчету коэффициент смещения Угол подъема линии витка червяка: на делительном цилиндре: на начальном цилиндре: Фактическое передаточное число: Полученное значение
3.7.2.4 Размеры червяка и колеса (см. п. 3.3, рис. 3.4) Диаметр делительный червяка: диаметр вершин витков: диаметр впадин: Длина
При положительном коэффициенте смещения ( Для фрезеруемых и шлифуемых червяков полученную расчетом длину Диаметр делительный червячного колеса: диаметр вершин зубьев: диаметр впадин: диаметр колеса наибольший: где Ширина венца: где
3.7.2.5 Скорость скольжения и КПД передачи Скорость скольжения в зацеплении:
где
m – модуль, мм;
Коэффициент полезного действия червячной передачи:
где
Меньшее значение
3.7.2.6 Силы в зацеплении (см. п. 3.4, рис. 3.5). Окружная сила на колесе, равная осевой силе на червяке:
Окружная сила на червяке, равная осевой силе на колесе:
Радиальная сила:
Для стандартного угла:
|

 червяка определяется в зависимости от передаточного числа:
червяка определяется в зависимости от передаточного числа: ,
, = 610 для эвольвентных, архимедовых и конволютных червяков;
= 610 для эвольвентных, архимедовых и конволютных червяков; – коэффициент концентрации нагрузки: при постоянном режиме нагружения
– коэффициент концентрации нагрузки: при постоянном режиме нагружения  .
. находят по графику (рис. 3.7), в зависимости от передаточного числа
находят по графику (рис. 3.7), в зависимости от передаточного числа  .
.
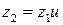 .
. 40…60.
40…60. ;
; .
. .
.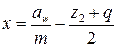 .
. > 1, 0, то изменяют
> 1, 0, то изменяют  ,
,  ,
, 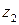 или q.
или q. ;
; .
. .
. не должно отличаться от заданного более чем на: 5% – для одноступенчатых и 8% – для двухступенчатых редукторов.
не должно отличаться от заданного более чем на: 5% – для одноступенчатых и 8% – для двухступенчатых редукторов.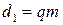 ;
;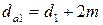 ;
; .
. нарезанной части червяка при коэффициенте смещения
нарезанной части червяка при коэффициенте смещения  :
: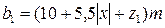 . (2)
. (2) ) червяк должен быть несколько короче. В этом случае размер
) червяк должен быть несколько короче. В этом случае размер 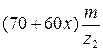 . Во всех случаях значение
. Во всех случаях значение  ;
; ;
;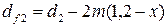 ;
; ,
, – для передач с эвольвентным червяком;
– для передач с эвольвентным червяком; 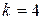 – для передач, нелинейчатую поверхность которых образуют тором.
– для передач, нелинейчатую поверхность которых образуют тором.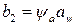 ,
, при
при  при
при  , где
, где 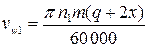 ,
, – окружная скорость на начальном диаметре червяка, м/с;
– окружная скорость на начальном диаметре червяка, м/с; – частота вращения червяка, об/мин;
– частота вращения червяка, об/мин; – угол подъема линии витка на начальном цилиндре.
– угол подъема линии витка на начальном цилиндре. ,
,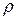 – приведенный угол трения, определяемый экспериментально с учетом относительных потерь мощности в зацеплении, в опорах и на перемешивание масла. Значение угла трения
– приведенный угол трения, определяемый экспериментально с учетом относительных потерь мощности в зацеплении, в опорах и на перемешивание масла. Значение угла трения  :
:


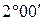
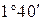
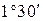





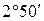

 .
. .
. .
. ,
,  .
.


